A través del espejo de las hojas de cálculo de Google con las fórmulas iterativas

Hacía tiempo que quería escribir unas líneas sobre esta marcianada que son las fórmulas iterativas, un tipo particular de expresiones francamente singular. Si ArrayFormula hizo en su momento que tus neuronas enloquecieran (como debe ser), espera a saber de qué va esto.

Pero dado que el concepto es extenso y ciertamente intenso, creo que será mejor que lo exploremos de manera experimental. ¿Estás listo? Pues venga, abre una nueva pestaña en tu navegador (si no es Chrome no pasa nada) y teclea en la barra de direcciones:

sheet.new

Comencemos por el principio.

La deliciosa normalidad de las hojas de cálculo

Es posible que alguien te haya hablado ya de algo llamado referencias circulares. Y te habrá aleccionado para que las evites a toda costa, ¿verdad?

Aquí, por ejemplo, usamos una fórmula en la celda A4 que utiliza el valor existente en A2 para realizar una operación. En este caso decimos que A2 es una celda precedente a A4 y que A4 es dependiente de A2.

Si estuviéramos usando Excel, su estupenda función de rastreo incluso nos pintaría unas bonitas flechas de colores para identificar las referencias a celdas precedentes y dependientes. En las hojas de cálculo de Google nos conformamos con apreciar los colorines al editar la fórmula, que tampoco está mal.

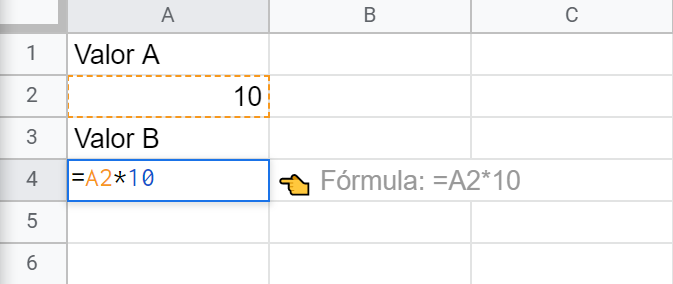
Si a continuación introducimos en A2 una fórmula que dependa del valor de A4 nos toparemos con lo que se denomina referencia circular. Un abrazo mortal... o como quieras llamarlo.

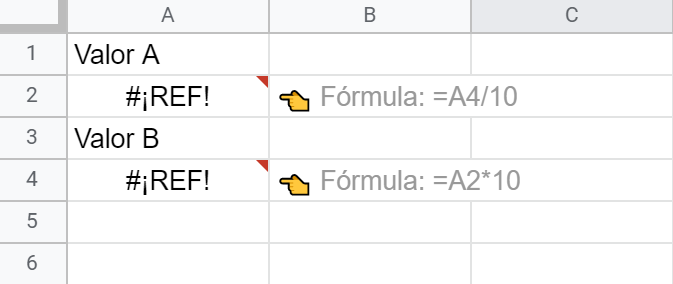
Y se desencadenará el por otra parte comprensible infierno de #¡ERRORES!. ¡Vade retro, referencias circulares!

En los cursos de iniciación a las hojas de cálculo suelen poner de cara a la pared con orejillas de burro durante horas, sosteniendo pesados manuales de Excel 97 sobre ambos brazos, a cualquier aprendiz que ose cuestionar la sacrosanta y ordenada secuencialidad de las expresiones de cálculo que entretejen los valores de las celdas y pergeñe expresiones como las de arriba. Y probablemente sea por una buena razón.

Pero si mueves graciosamente el ratón sobre A2 o A4 verás este sugerente mensaje de error en un panel emergente:

Esta enigmática perorata parece indicar que, más allá de nuestra tranquilizadora normalidad, existe una realidad oculta, alternativa, repleta de esos inefables cálculos iterativos, reservada a los valientes que estén dispuestos a arriesgar su salud mental, cual investigadores en una aventura de La Llamada de Cthulhu prestos a hacer sus tiradas de cordura en dado 100 a la menor indicación del Director de Juego.

¿Estás listo para conocer la verdad? Atravesemos pues el espejo en busca de ella.

Los perturbadores cálculos iterativos

No borres aún tus fórmulas circularmente referenciales.

👉 Haz clic en Archivo ⇒ Configuración de la hoja de cálculo y, a continuación, dirígete a la pestaña Cálculo.

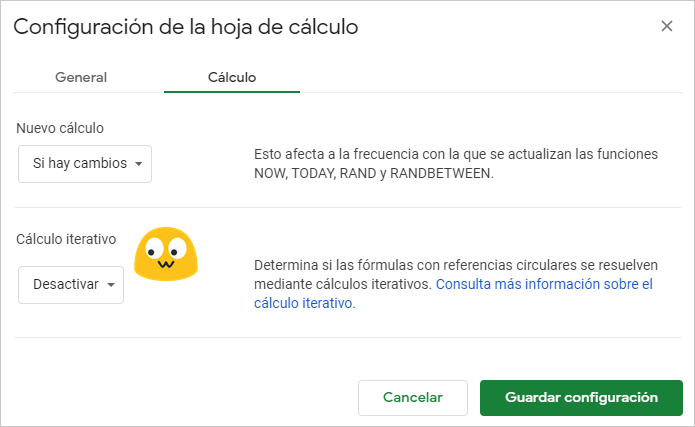
👉 Ahora activa los cálculos iterativos. Que no te tiemble la rata.

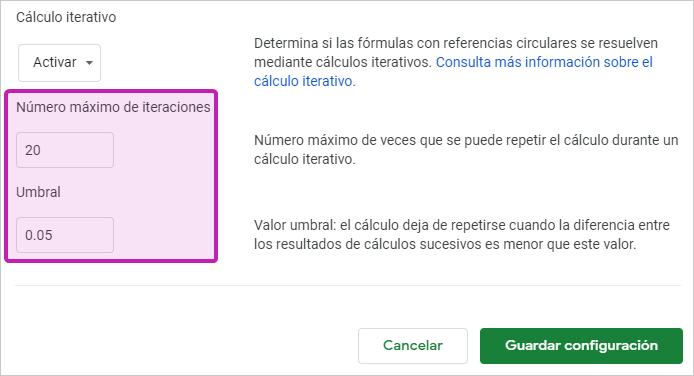
Al hacerlo comprobarás que aparecen dos nuevas opciones:

• Número máximo de iteraciones.
• Umbral.

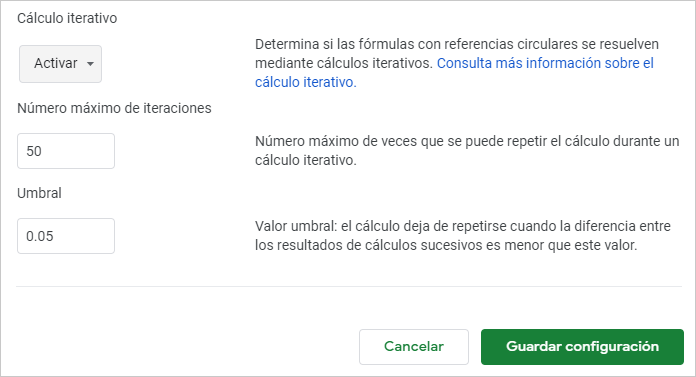
Por el momento los valores por defecto nos valen. Haz clic en Guardar configuración y metámonos de cabeza en la madriguera del conejo blanco.

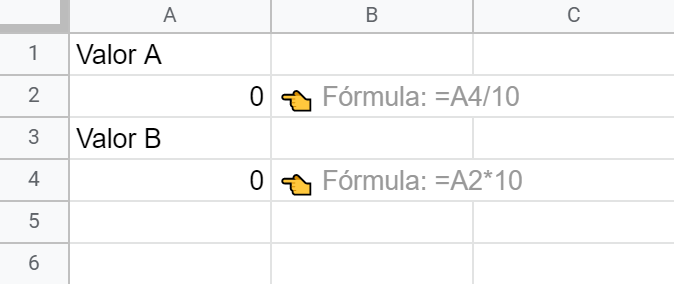
¿Ni rastro de los errores debidos a las referencias circulares? ¿Ceros? ¿Pero qué brujería es esta?

👉 Para entender lo que ha pasado vas a hacer una cosa. Bueno, dos:

1. Introduce el valor 10 en la celda A2.
2. A continuación, sustituye el 10 por la fórmula =A4/10.

Si, no es una errata ni me está afectando el calor estival. Primero un 10, luego la fórmula otra vez. Y mira qué ocurre después:

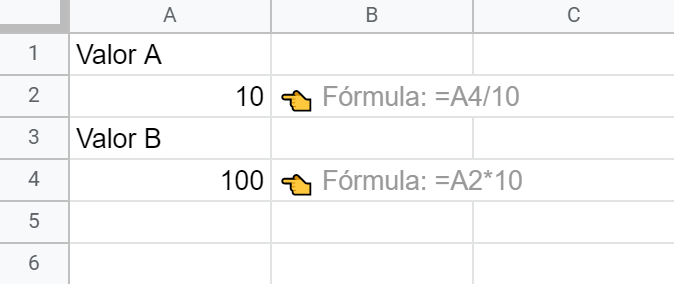
Hasta el mismísimo Maurits Cornelis Escher asentiría con aprobación al verlo. Esto es como tratar de sujetarse a uno mismo en el aire apoyando los pies en las propias manos, ¿verdad? Solo que aquí parece funcionar. Nuestras fórmulas con referencias circulares no arrojan ya errores espantosos.

¡Enhorabuena, has llegado al País de las Maravillas!

Quién eres tú y qué has hecho con mis fórmulas

Bueno, vale, esto mola. Pero ¿para qué sirve? Para muchas cosas, pero calma. Aún tenemos que entender bien cómo funciona y qué utilidad tienen los ajustes número máximo de iteraciones y umbral.

¡Averigüémoslo!

👉 Crea una pestaña nueva en la hoja de cálculo e introduce esta sencilla fórmula en A1:

= A1 + 1

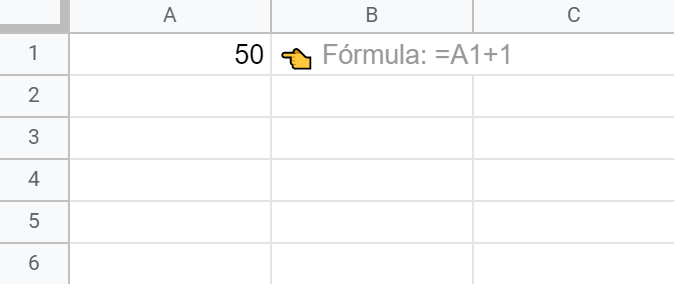
El resultado es 50.

👉 Sustituye la fórmula en A1 por:

= A1 + 2

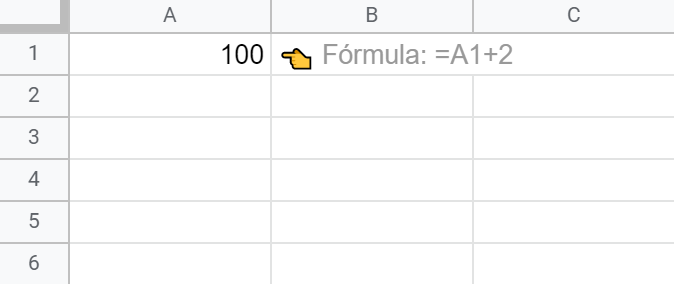
Verás que ahora el resultado es 100.

En cada ocasión la fórmula se ha evaluado 50 veces, sumando 1 o 2 respectivamente al valor previo de la celda A1 de manera iterativa, que no es sino una forma sofisticada de indicar que el cálculo se repite un número determinado de veces. ¿Te suena de algo ese 50? ¡Buena memoria!

1️⃣ Lección 1️⃣
El valor establecido para el ajuste del número máximo de iteraciones determina cuántas veces se repetirá el cálculo de la fórmula antes de detenerse y devolver un valor definitivo.

👉 Regresa a los ajustes de los cálculos iterativos (recuerda, Archivo ⇒ Configuración de la hoja de cálculo ⇒ Cálculo) e introduce en esta ocasión un valor de 20, a ver por dónde sale la cosa:

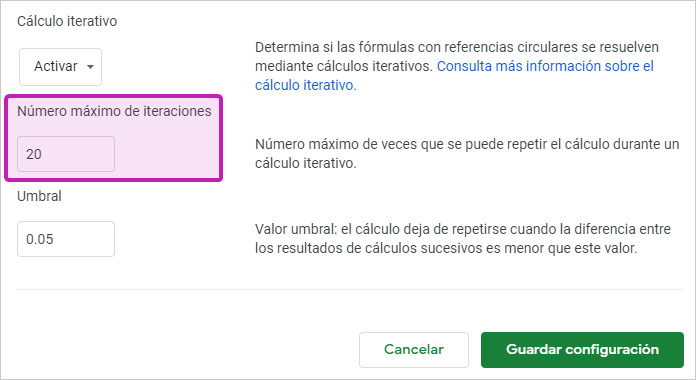
Y la cosa sale por aquí:

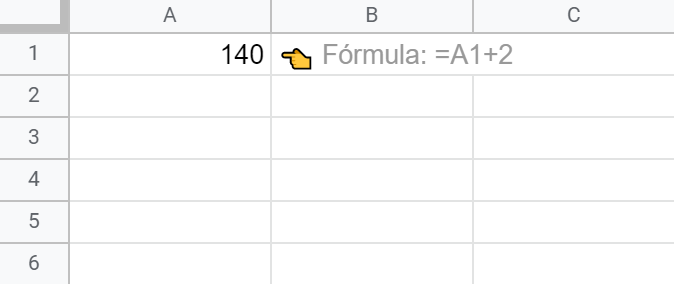
Partíamos de un valor de 100 en A1. Al establecer en 20 el nº máximo de iteraciones se deben recalcular las fórmulas, pero esta vez solo se han practicado 20 repeticiones. El valor final es por tanto 100 + 20 x 2 (140).

¿No es esto hermoso?

👉 Prueba a escribir ahora cualquier cosa en la celda A2. Un simple Hola bastará.

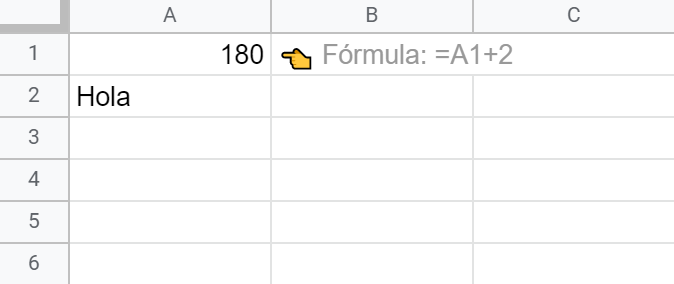
¡Toma ya! El valor se ha recalculado nuevamente y es ahora 180 (140 + 20 x 2).Y esto nos lleva a la...

2️⃣ Lección 2️⃣
Los procesos de cálculo iterativo en las celdas que contienen fórmulas con referencias circulares se desencadenarán cada vez que se modifique el valor de cualquier celda de la hoja de cálculo, aunque no se trate de una precedente, o cuando se produzca un recálculo general de la hoja por otros motivos.

Si estás pensando en que esto de que las fórmulas que se resuelven de manera iterativa se recalculen aunque ninguna de sus celdas precedentes hayan cambiado va a ser un problema, tienes razón. Pero de eso hablaremos más tarde.

Vamos a jugar a continuación con el otro parámetro de configuración de los cálculos iterativos. Me refiero al umbral.

👉 Cambia el 0.05 (ojo, el separador decimal debe ser un punto) por un 3.

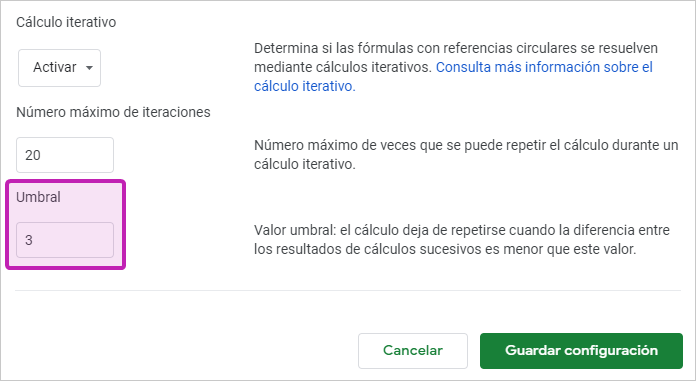
Volvamos nuevamente a la hoja, a ver qué maravillas nos aguardan en ella.

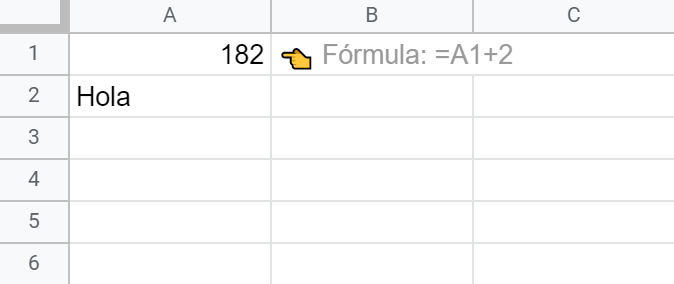
¿Sorprendido? No deberías (seguro que has leído el texto a la derecha del ajuste sobre el que hemos intervenido). Esto es lo que ha pasado:

1. La fórmula se ha recalculado en una 1ª iteración (180 + 2 = 182).
2. Como el valor más reciente (182) menos el inmediatamente anterior (180) es inferior al umbral que has establecido (2 < 3) el cálculo iterativo se detiene.

👉 Escribe ahora algo como Adiós en A2. Seguro que ya intuyes lo que viene a continuación.

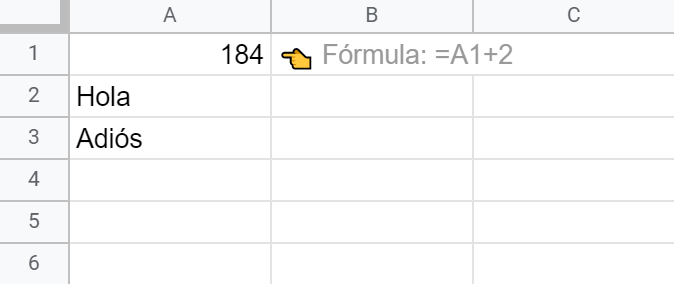
Como era de esperar, el cambio en el valor de una celda, aunque no sea un referencia en la fórmula de A1, pone en marcha nuevamente el proceso de cálculo iterativo, que no obstante finaliza nuevamente tras un solo paso de cálculo como consecuencia del umbral que has establecido en 3.

Ya podemos cerrar con la...

3️⃣ Lección 3️⃣
El cálculo iterativo se detiene cuando la diferencia entre los valores obtenidos en dos iteraciones consecutivas es inferior al umbral establecido.

Por tanto, ambos ajustes (nº de iteraciones y umbral) son algo así como el limitador de velocidad de un vehículo, solo que aquí pilotamos una hoja de cálculo en lugar de un automóvil y nos preocupa el tiempo de ejecución en lugar del que nos cuesta llegar al destino.

Después de todo, no sería razonable permitir que estos cálculos se ejecutaran indefinidamente, consumiendo eventualmente recursos del sistema (memoria y tiempo de proceso) sin control.

Mediante este mecanismo de control tenemos al menos la garantía de que las fórmulas dejarán de evaluarse en algún momento y ofrecerán un resultado más o menos aproximado, dependiendo del número de iteraciones realizadas, al valor perseguido.

Si eres matemático o financiero, desconocías esta capacidad de las hojas de cálculo y has llegado hasta aquí, seguramente estarás ya pensando en todas las posibilidades que se abren. Cosas como el cálculo de intereses y capitales y muchas series matemáticas pueden resolverse de manera iterativa, con una sola fórmula, en lugar de construyendo largas tablas de datos con cálculos intermedios (lo que no deja de ser una iteración explícita, claro).

Resumamos en un pispás todo lo aprendido en un orden más apropiado.

Quédate con esto:

1. El número máximo de iteraciones determina cuántas veces se repetirá el cálculo de la fórmula antes de detenerse y devolver un valor definitivo.
2. El cálculo iterativo finalizará también en cuanto la diferencia entre los valores obtenidos en dos iteraciones consecutivas sea menor que el umbral establecido.
3. Los procesos iterativos se desencadenan cada vez que se modifica el valor de cualquier celda o cuando se produce un recálculo general de la hoja por otros motivos.
4. Y una cosita más que no te había contado hasta ahora por aquello de no marear: Los ajustes sobre los cálculos iterativos se establecen de manera general sobre todas las pestañas de la hoja de cálculo. Si usas fórmulas con referencias circulares con distintos requerimientos por lo que hace a los ajustes de nº máximo de iteraciones y umbral la cosa se puede poner fea.

Te entiendo. Estas reglas de juego te han de resultar necesariamente desconcertantes si nunca antes habías oído hablar de cálculos iterativos. Pero tienen cierto sentido, ¿verdad? (dime que sí, por favor).

Bien, parece por tanto que ya tenemos limitador de velocidad, pero nos faltan aún el freno de mano, el GPS y la llave de contacto de nuestro itinerante y muy particular vehículo iterativo. Sigue conmigo para ver de dónde los sacamos.

¿Lo puedes hacer más despacio?

Huelo cierto recelo a todo este tinglado iterativo.

Tal vez te gustaría ver el mecanismo en tiempo real. No sé, para acabarlo de creer y todo eso.

Resulta que gracias a la relativamente baja velocidad de computación de nuestras por otra parte idolatradas hojas de cálculo de Google, puedes.

Pero nos vamos a tener que poner un pelín matemáticos, porque el ejemplo que te he preparado lo requiere.

¿Conoces la serie armónica? Se calcula sumando los elementos de una sucesión que resulta muy natural, tal que así:

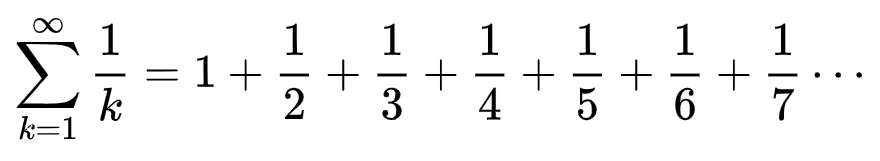
Pues vamos a trabajar con una prima hermana suya, denominada serie armónica alterada: 

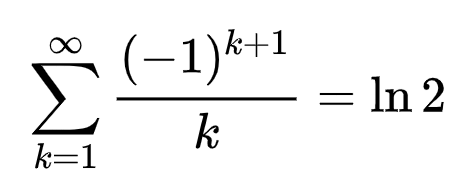
En esta segunda serie los elementos de la sucesión que se obtienen cuando k es impar se suman, en tanto que los impares se restan. ¡Y va y resulta que lo que sale se va aproximando progresiva pero inexorablemente al logaritmo natural de 2!

Nota: Si crees que esto de las hojas de cálculo y los scripts es lo más de lo más, espera a profundizar en el alucinante mundo de las series (matemáticas, no de Netflix), en sus propiedades de convergencia o divergencia. Lee algo de Euler o Gauss y entonces sí fliparás, pero de verdad. Échale un vistazo a Gaussianos y luego me cuentas.

Como esos ∞ sobre las sigmas mayúsculas dejan bien claro, estas series tienen un número infinito de términos. Vamos a calcular y sumar algunos de los que construyen la serie armónica alterada. Y lo haremos de dos maneras distintas:

1. Del modo tradicional.
2. Usando cálculos iterativos.

👉 ¡Que el ritmo no pare! Crea una nueva pestaña en tu hoja de cálculo. Añade una primera columna con los valores de k. No te pases, entre 1 y 20 será suficiente.

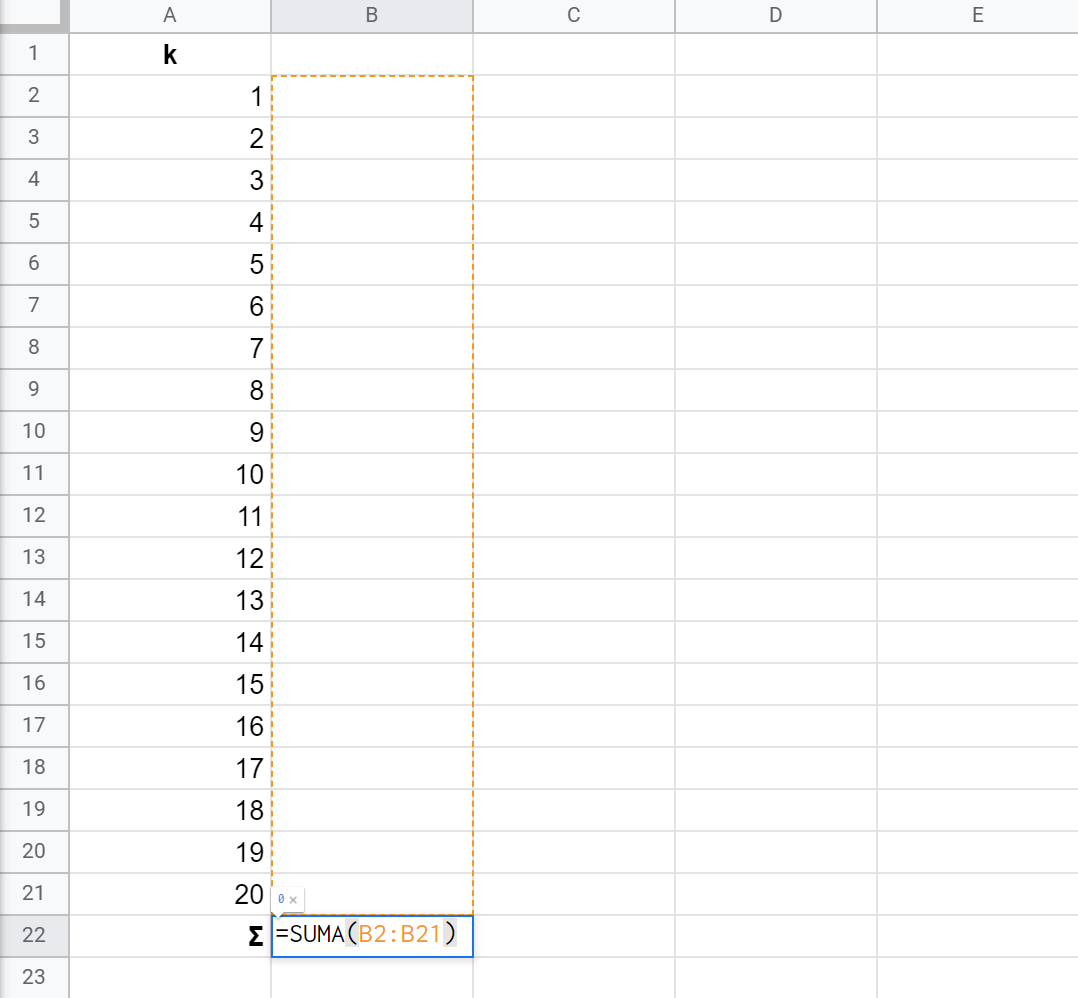
👉 Suma en B22 todos los elementos de la sucesión. Sí, ya sé, ahí no hay nada (aún). Es por darle un poco de misterio.

= SUMA( B2:B21 )

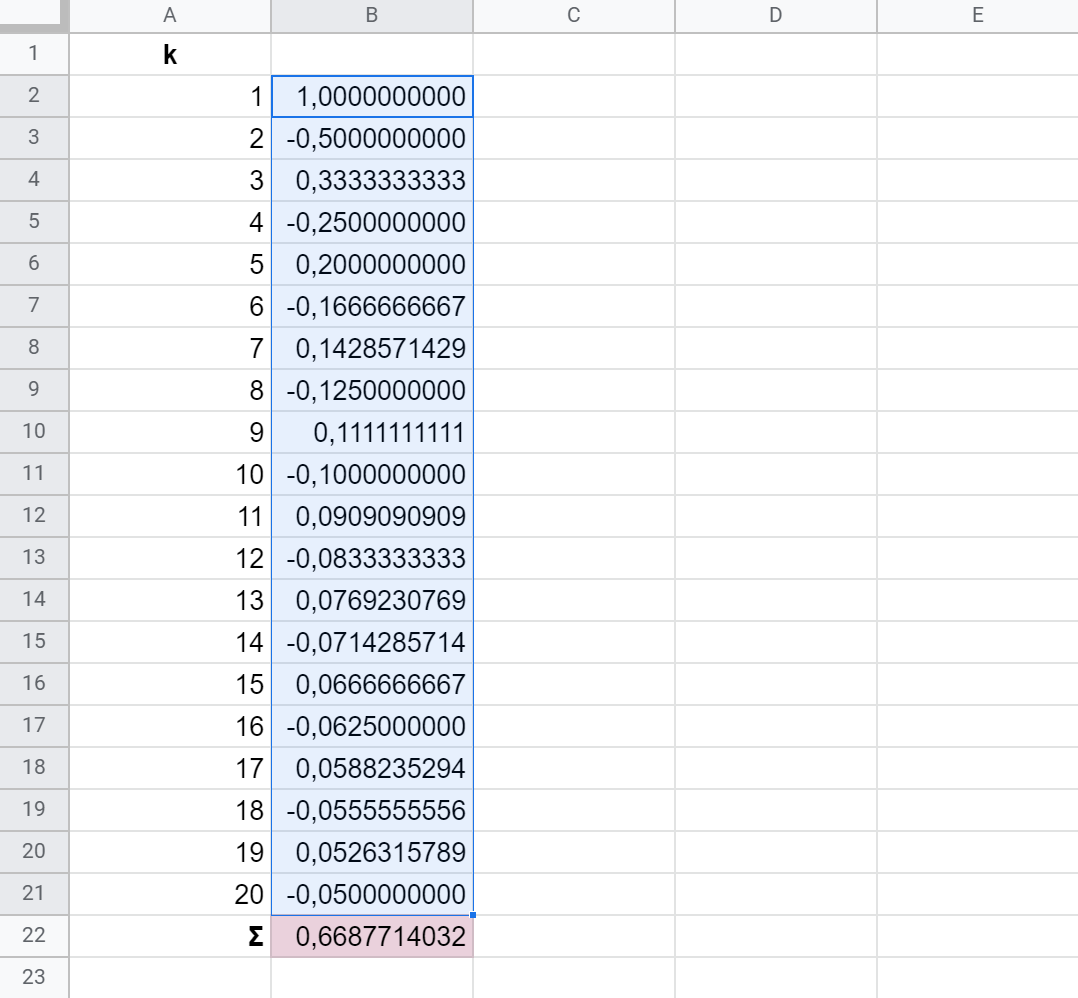
👉 Ahora introduce la siguiente fórmula en B2:

= SI( ES.IMPAR( A2 ) ; 1/A2 ; -1/A2 )

Puedes comprobar que esta expresión generaliza el cálculo del término k de la sucesión que genera la serie armónica alterada. Los términos pares se restan, los impares se suman.

Solo tienes que arrastrarla hasta B21 para calcular los 19 elementos restantes.

👉 Para validar el resultado, calcula el logaritmo natural de 2 en B1:

= LN( 2 )

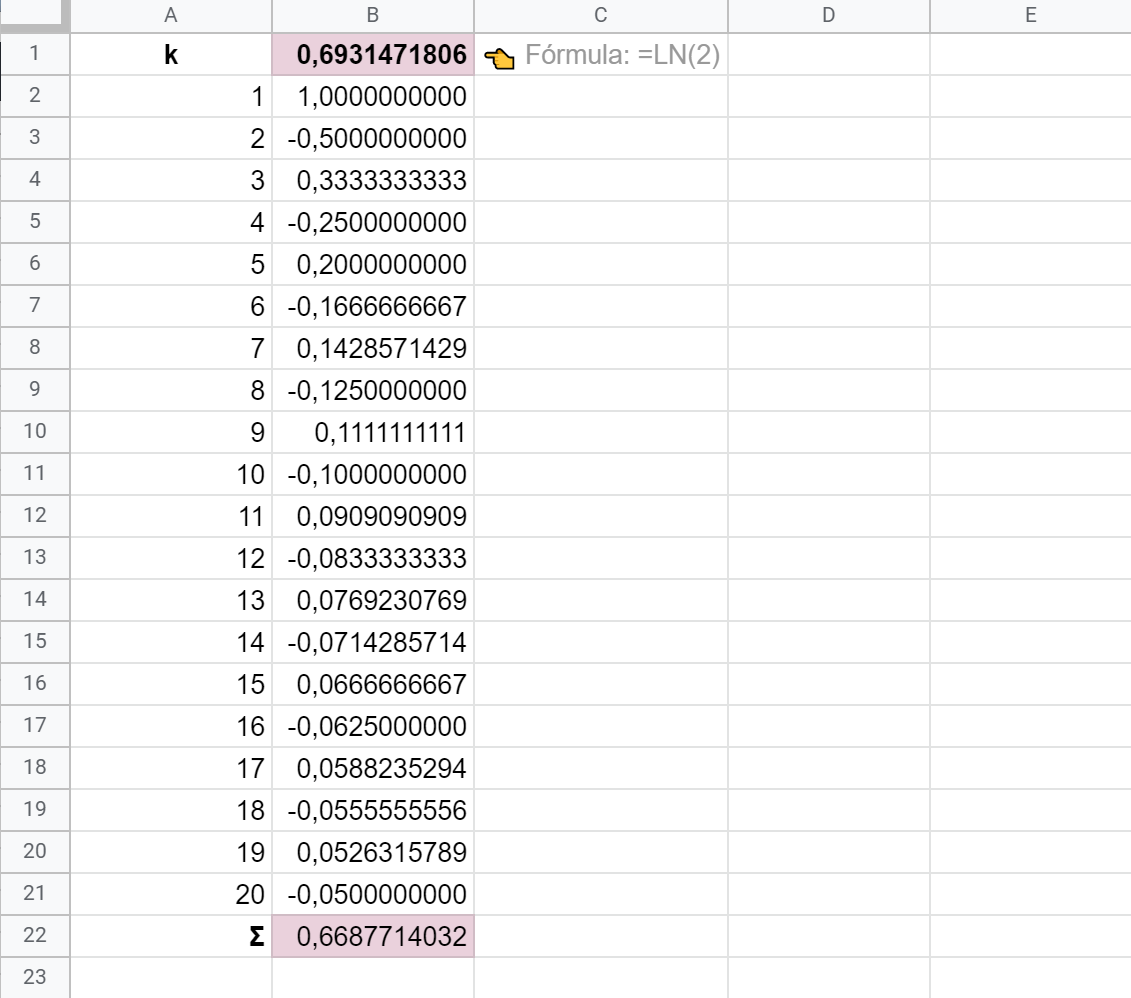
Hemos calculado la serie armónica alterada con sus 20 primeros elementos. A medida que añadiéramos más términos a la sucesión (k mayor), la suma final tendría paulatinamente más valores y su suma convergería mejor hacia la magnitud real calculada en B1.

Así son las series.

¿Lo resolvemos también con cálculos iterativos? Al lío.

Aquí la filosofía cambia. Pero mucho:

• Por un lado, necesitamos una celda que vaya representando los distintos valores sucesivos de k.
• Por otro lado, la fórmula que escribiremos en una segunda celda deberá utilizar los valores de k para calcular los términos correspondientes de la sucesión y realizar la suma parcial de modo iterativo.

Lo importante es que las fórmulas de ambas celdas dependan la una de la otra para que la estrategia iterativa que resuelve el cálculo haga su magia.

Lo sé, un poco comecocos.

Pero antes de seguir, comprueba que el número máximo de iteraciones es 20 y el umbral 0.05 (seguro que a estas alturas los has tocado mil veces).

Bien, vamos a montar nuestro tinglado de cálculo en las celdas D19 y D22. Comencemos por la celda que representará la posición del elemento de la serie que debe calcularse justo a continuación.

👉 Escribe en D19 esta fórmula:

= SI( D22=0 ; 1 ; D19+1 )

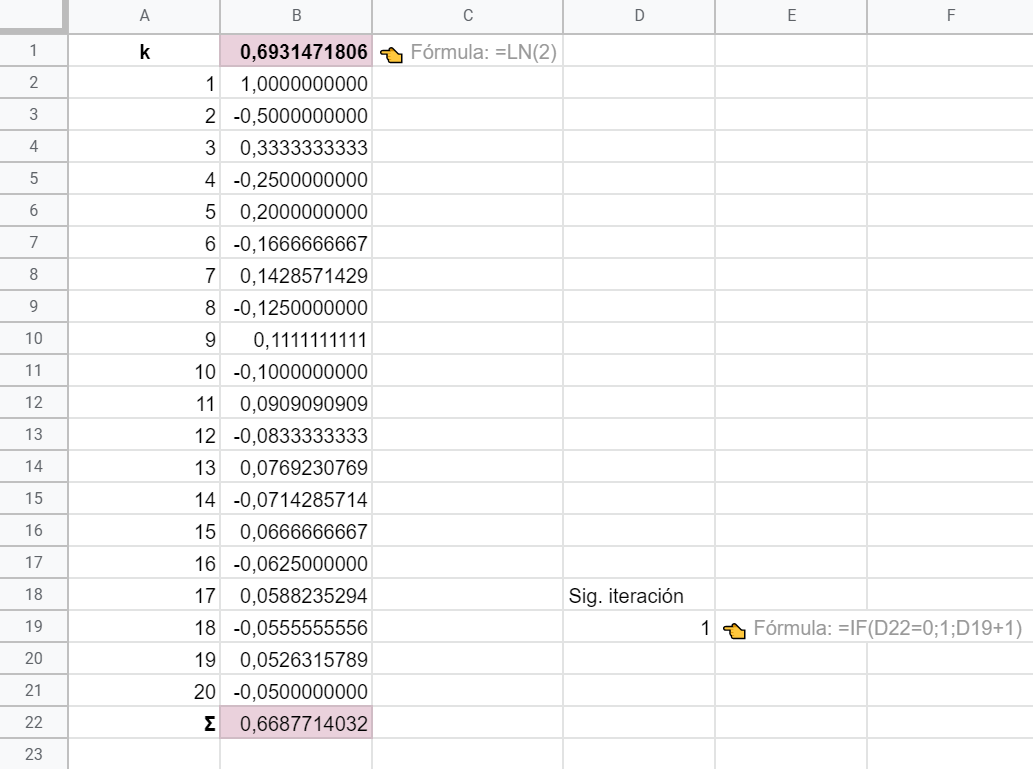
Fíjate bien, esta fórmula impide que el proceso iterativo arranque en tanto el valor de la serie, que se calculará en D22, sea 0 (una celda vacía se evalúa como 0). Además, constituye nuestro GPS, dado que nos chiva en qué iteración nos encontramos en cada momento. Esencialmente, D19 representa a la variable k.

👉 Escribe en D22 esta otra fórmula, que es la que va a sumar todos los términos de la sucesión numérica:

= SI( D19=1
      ; 1
      ; SI( ES.IMPAR( D19 ) ; D22+1/D19 ; D22-1/D19 )
    )

Con la primera función SI se genera el término inicial (1) de la sucesión de valores.

El segundo SI simplemente calcula y suma o resta al valor acumulado el del elemento que se halla en la posición k, dependiendo de que esta sea impar o par, respectivamente.

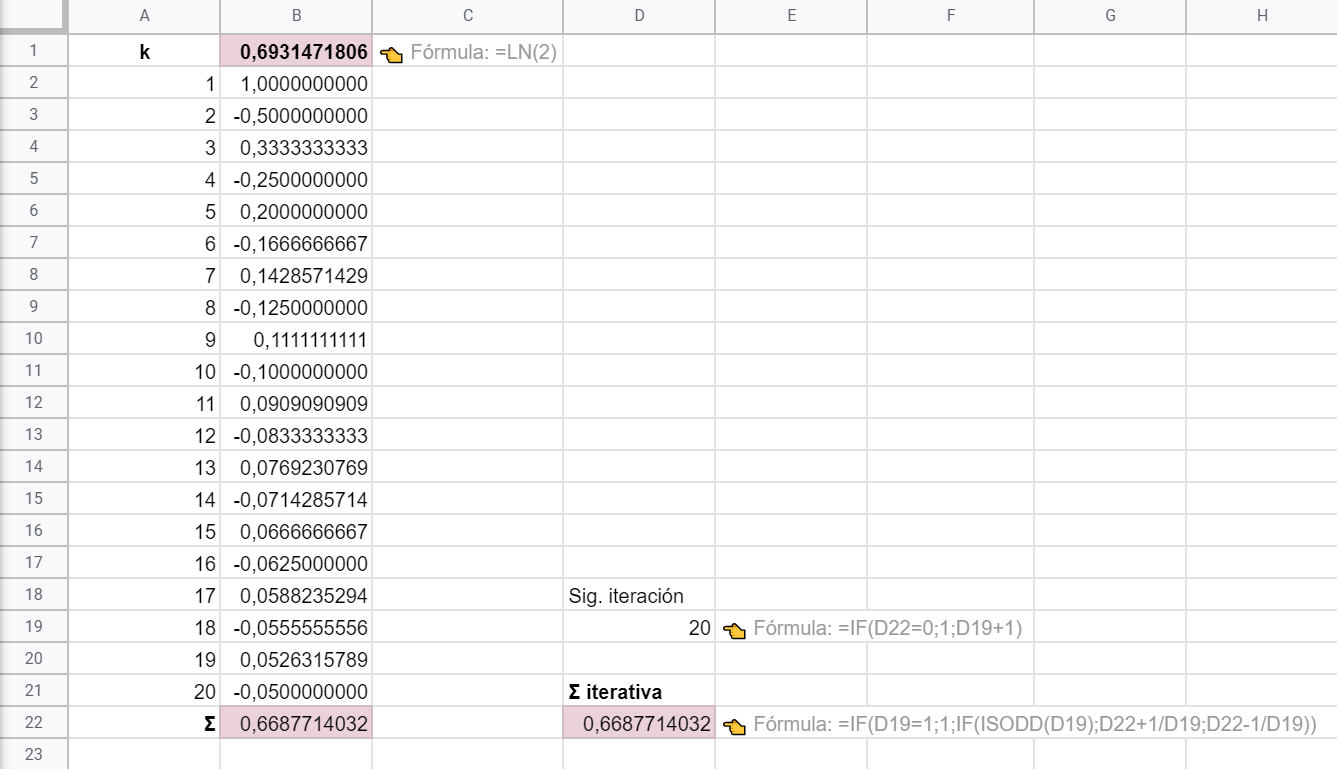
Como puedes ver, el resultado es idéntico al obtenido en la celda B22 usando la estrategia de cálculo convencional que hemos utilizado en primer lugar. Esto no debe extrañarte, solo hemos variado el método de cálculo, pero las iteraciones son las mismas en ambos casos.

Las Matemáticas no fallan (las personas que las utilizan sí, claro).

Pero te había prometido al inicio de esta sección que ibas a poder sentir de cerca en tu cara, digo hoja de cálculo, toda la fuerza endiablada del viento iterativo.

👉 Prueba esto:

1. Corta (y elimina) la fórmula de D22.
2. Configura la hoja de cálculo para que no sean 20 sino 10.000 iteraciones, el valor máximo admitido, las que calculen el logaritmo natural de 2. ¡Vamos con todo!
3. Pega la fórmula de nuevo en D22.

Contempla el resultado. No, no hay ningún Apps Script por detrás dándole vidilla a esto.

Esas 10.000 iteraciones le han pesado al motor de cálculo, que parece estar un poco fondón. Y precisamente por eso hemos podido ver en directo cómo las sumas parciales se iban aproximando progresivamente al objetivo, el valor real del logaritmo natural de 2.

Como era de esperar, la exactitud del valor calculado de este modo es proporcional al número de elementos de la sucesión que se han tenido en cuenta, lo que se corresponde de manera directa con el número de iteraciones realizadas, como ya sabemos. Disculpa que sea tan pesado con esto, pero me parece un concepto clave que debes hacer tuyo cuanto antes pera que todo encaje en tu cabeza.

¿Pero no te parece que eso de tener que andar borrando y reescribiendo fórmulas es poco práctico, a la par que nada elegante?

Además, hay otra razón de peso para no hacerlo. Repasemos las dependencias que hemos introducido en las fórmulas usadas en D19 y D22:

• D19 depende de D22 y de su propio valor.
• D22 depende de D19 y también de su propio valor.

Un lío cuyo correcto funcionamiento es extremadamente sensible al modo en que se hayan construido las condiciones de “contención” (las cláusulas de guarda de los IF) y al orden en que se introduzcan las fórmulas en cada celda. Ambos factores deben estar perfectamente engranados para que las referencias circulares se resuelvan iterativamente en la secuencia correcta para alcanzar el resultado buscado.

Y es que, amigo o amiga, las fórmulas con referencias circulares son temperamentales. Mucho. Y si no me crees, prueba tú mismo con otras expresiones similares a las que hemos usado en este apartado. Con esta en D19, por ejemplo:

= SI( NO( ESNUMERO( D22 ) ) ; 1 ; D19+1 )

Si introduces primero la fórmula en D22 y posteriormente la de D19 las cosas irán bien. Pero si osas hacerlo al revés el cálculo será incorrecto. Te dejo como ejercicio rompe mentes que averigües el porqué.

Por suerte podemos mejorar este estado de cosas. Busquemos esa llave de contacto 🔑.

El discreto encanto de las casillas de verificación

¿Aún sigues aquí? Estupendo. Se nota que te va el lío. A mi también.

No es de recibo tener que editar alguna de las celdas interdependientes para controlar el proceso de cálculo iterativo.

¡Necesitamos un mecanismo manual que permita inhibir y reiniciar los cálculos iterativos en determinadas celdas!

¿Un botón de puesta en marcha y reset? Justo eso buscamos.

Y una de las mejores maneras que se me ocurre de conseguirlo son las amistosas a la par que enormemente versátiles casillas de verificación  ☑️, el mejor invento desde el yogur griego con stracciatella de... (omito la marca que no me subvencionan).

¿Estás listo para modificar el modelo de cálculo anterior?

👉 Restaura los ajustes de cálculo iterativo (20 iteraciones, umbral de 0.05):

👉 Duplica la hoja en la que estabas trabajando, elimina las fórmulas en D19 y D22 e inserta una casilla de verificación en la celda D16 (Insertar ⇒ ☑ Casilla de verificación).

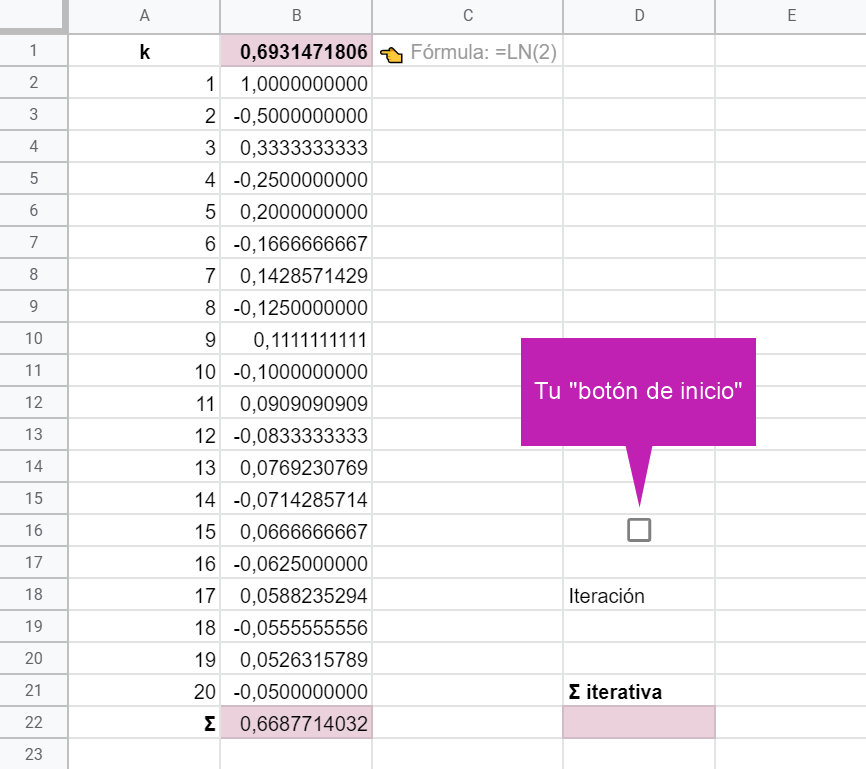
Ahora haremos depender el “arranque” del cálculo del estado de esta casilla de verificación.

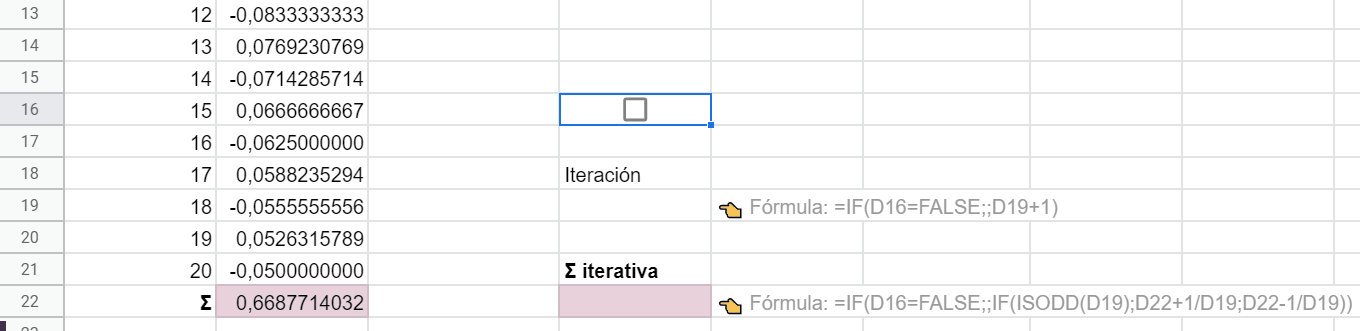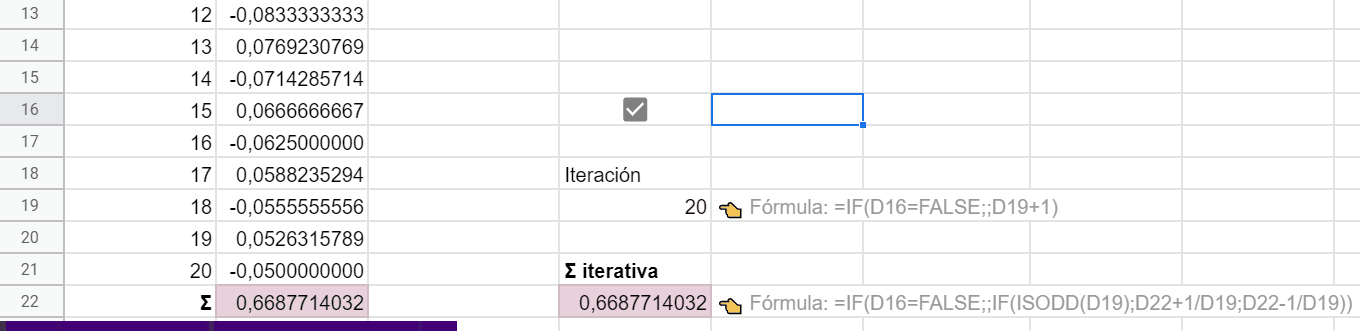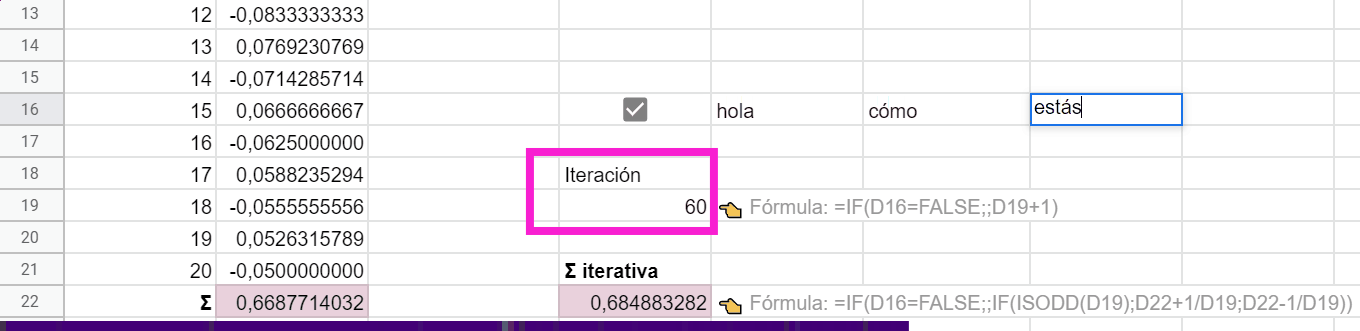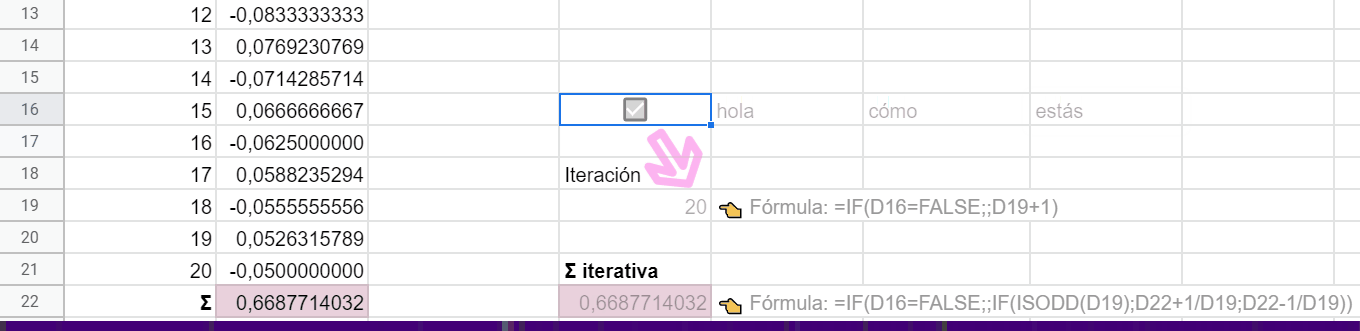
👉 Comencemos por la celda D19. Introduce esta fórmula:

= SI( D16=FALSO ; ; D19+1)

👉 Haz algo parecido con la fórmula en D22:

= SI( D16=FALSO
      ;
      ; SI( ES.IMPAR( D19 ) ; D22+1/D19 ; D22-1/D19 )
    )

También podríamos haber optado por que solo una de las fórmulas dependiera del estado de la casilla de verificación y la otra, a su vez, de la primera.

Pero precisamente porque recurrimos a una casilla de verificación para controlar el cálculo somos capaces de romper la interdependencia mutua que aparecía en los ejemplos anteriores, en los que cada celda tenía como precedente a la otra de manera recíproca.

En mi opinión esto resulta notablemente más intuitivo y reduce la posibilidad de que se deslicen errores, a veces difíciles de detectar, en ese delicado engranaje iterativo del que te hablaba en la parte final del apartado anterior.

No podemos evitar, sin introducir más condiciones un tanto artificiosas, que al escribir en otras celdas el cálculo prosiga desde donde se quedó. Pero con la casilla de verificación está chupado hacer borrón y cuenta nueva.

Control de presencia (iterativo) con marcas de tiempo

Entenderé que a estas alturas te sientes un poco como Steve Rogers o Wanda Maximoff. La resolución iterativa de fórmulas con referencias circulares nos dota de magníficos superpoderes hojacalcúlicos.

¿Te lo demuestro?

Con esos poderes podemos hacer virguerías como esta lista desplegable en la que los elementos van desapareciendo a medida que se van seleccionando:

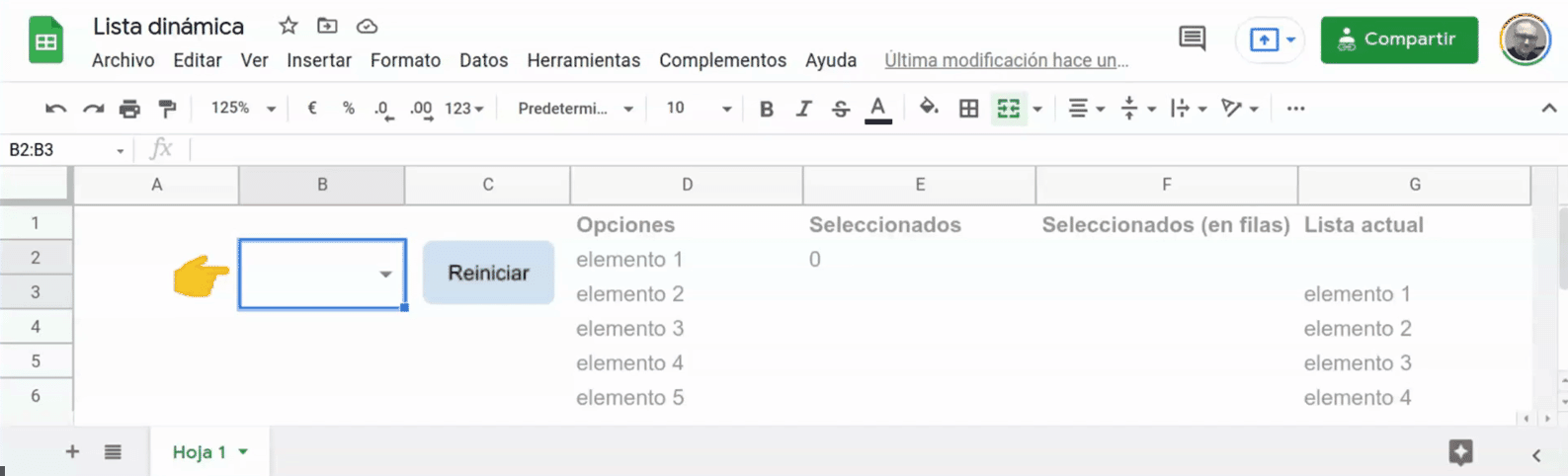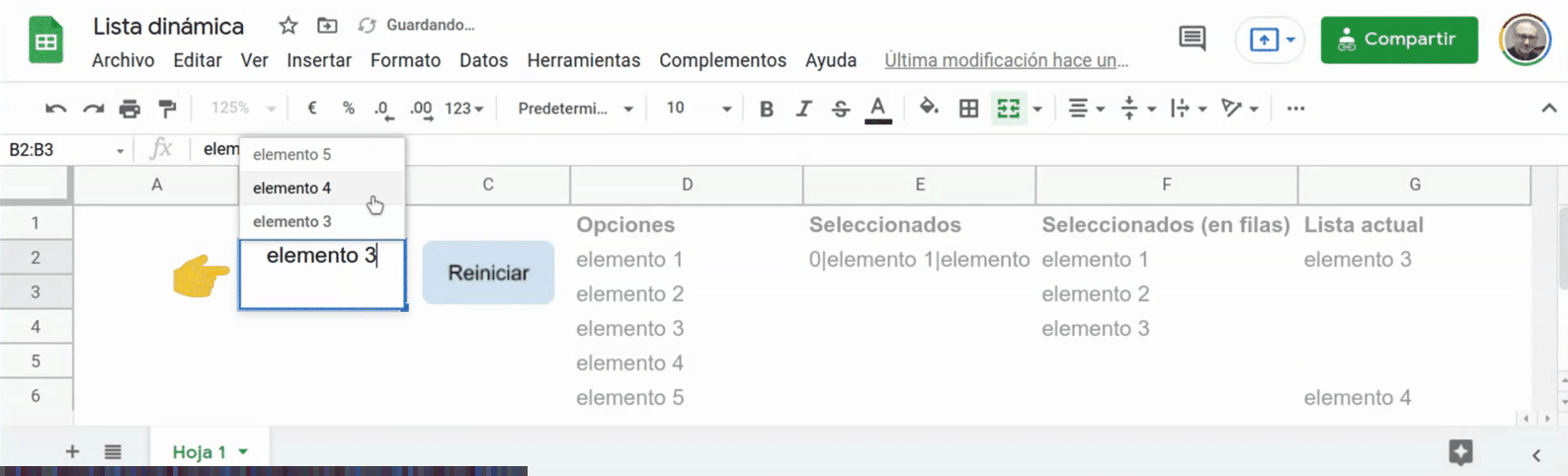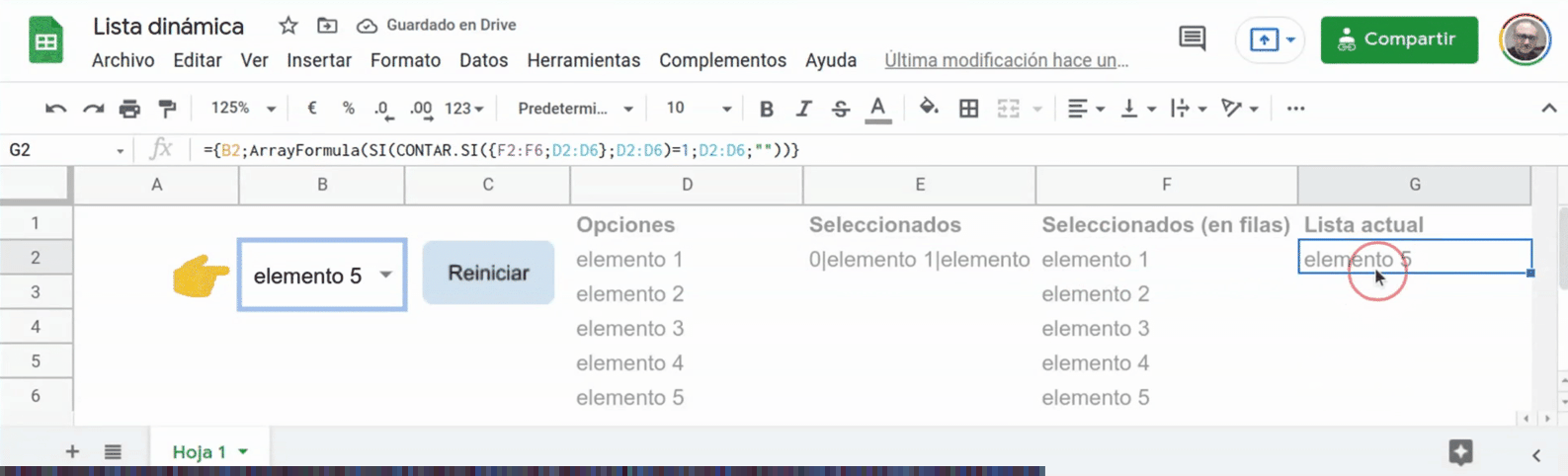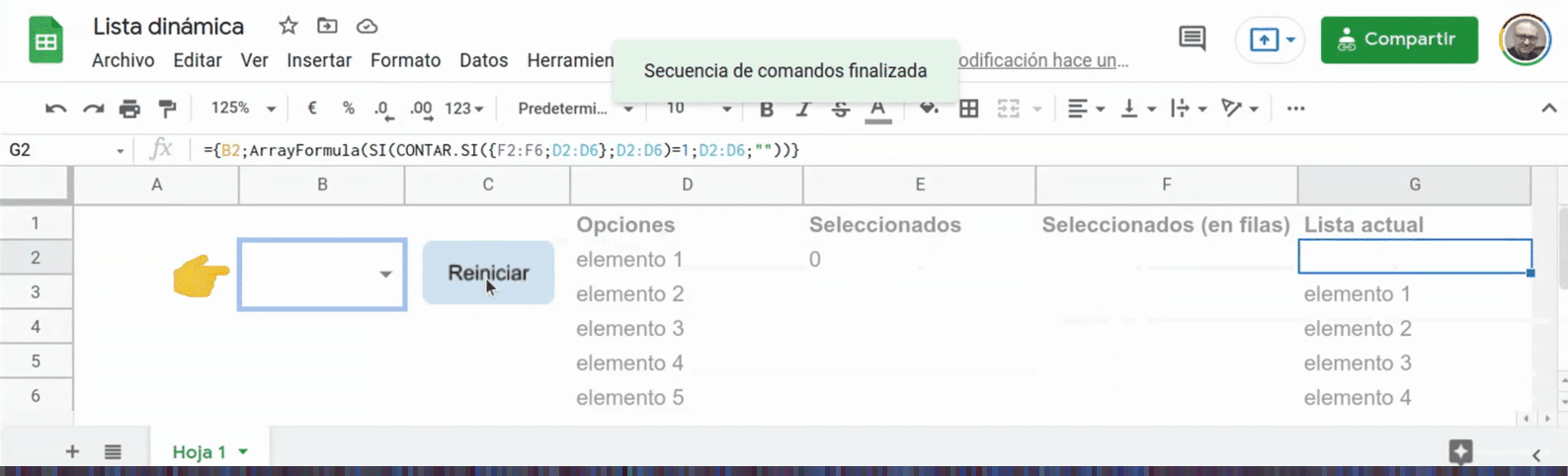
Aquí tienes la plantilla para que puedas destriparla concienzudamente.

Y también somos capaces de implementar un control de presencia, por ejemplo de los asistentes a una sesión de formación, registrando automáticamente la hora de entrada y de salida de cada participante para calcular su tiempo efectivo de asistencia.

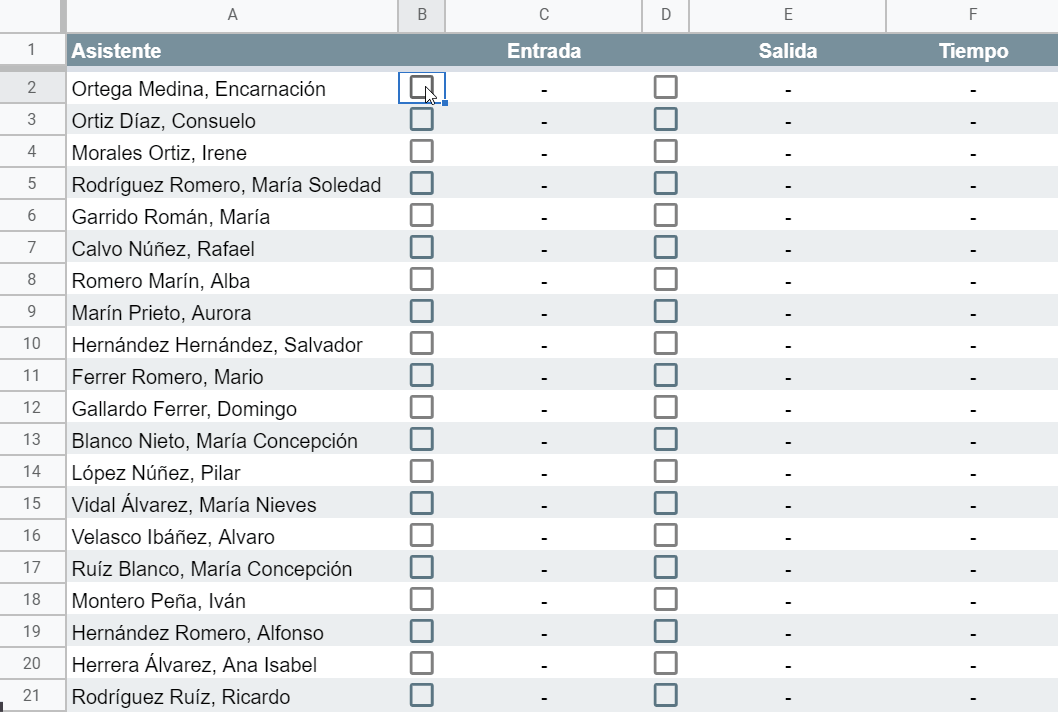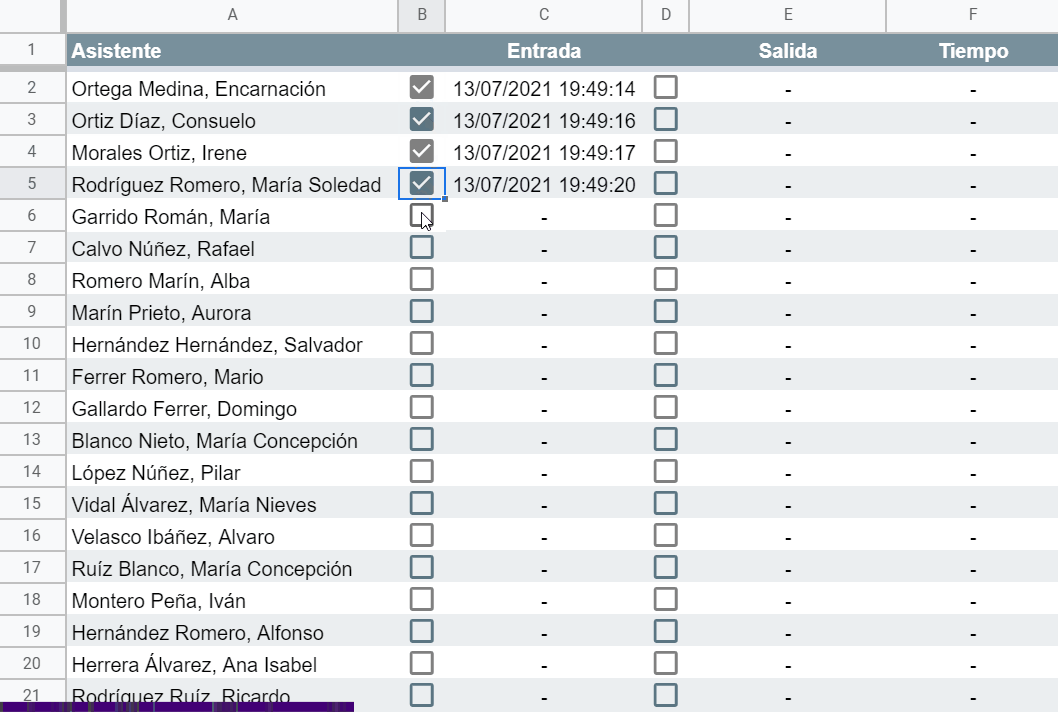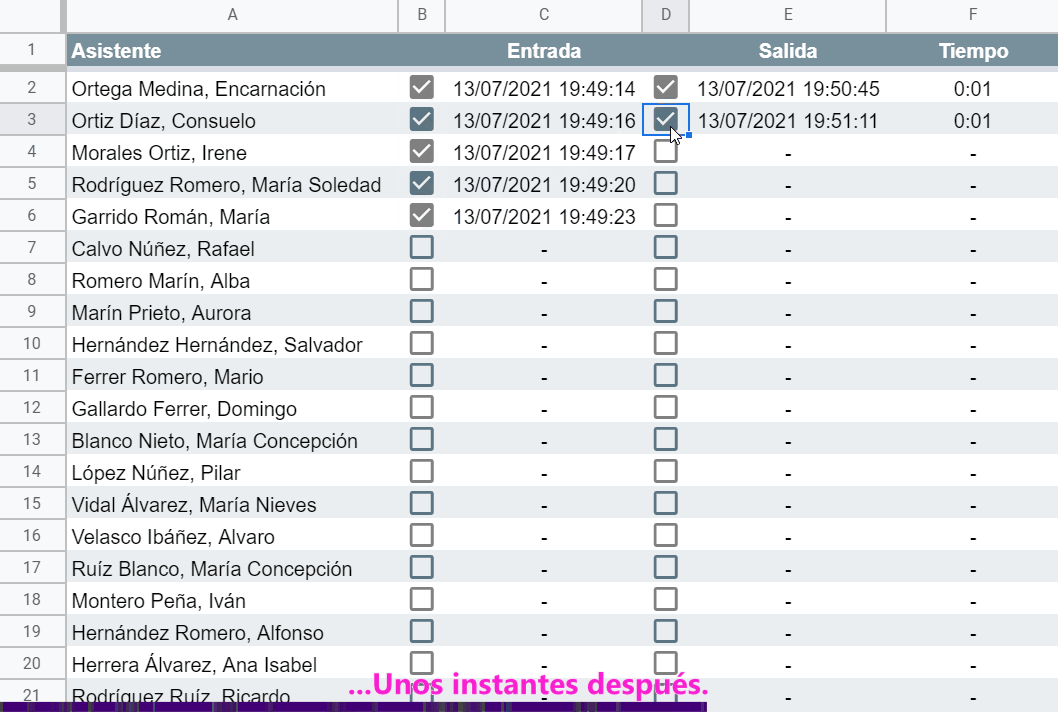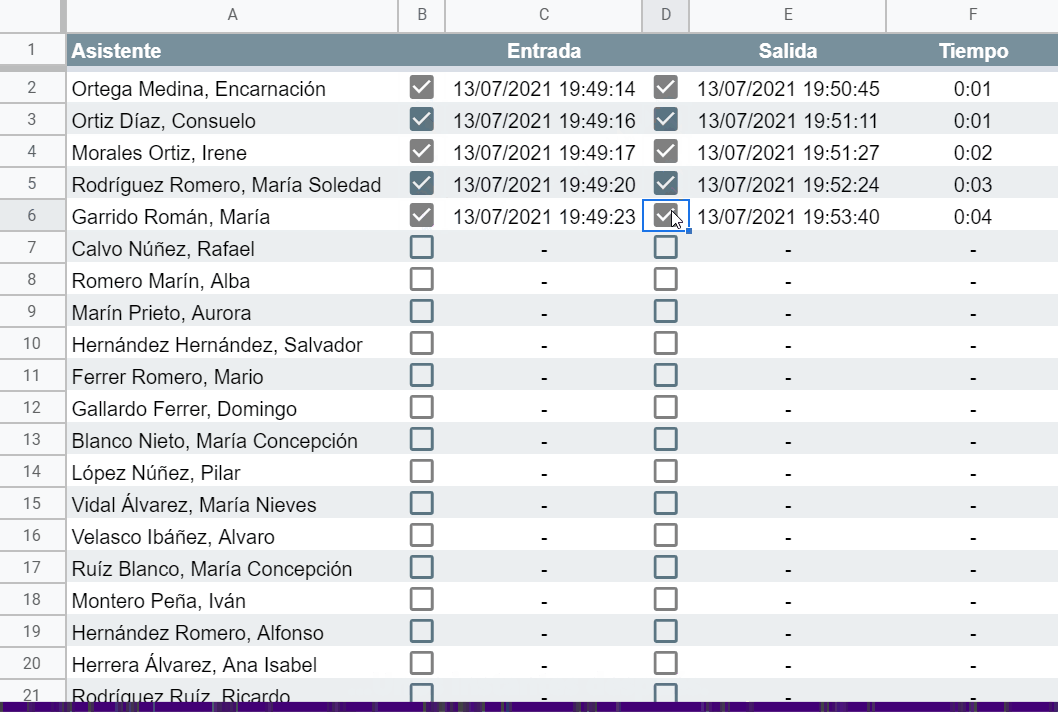
Echémosle un vistazo a la fórmula utilizada en las columnas C y E (idénticas) de este segundo ejemplo súper poderoso:

= ArrayFormula(
    SI( A2:A=""
        ;
        ; SI( B2:B=FALSO
              ; "-"
              ; SI(C2:C="-" ; AHORA() ; C2:C)
            )
      )
  )

Pasito a pasito y para cada fila en C2:C y E2:E:

1. Si en la columna A no hay texto (sin asistente en esa fila), la fórmula no devuelve ningún resultado (cuidadín, ningún resultado no es lo mismo que una cadena vacía).
2. Si tenemos asistente pero la casilla de verificación justo a la izquierda no está marcada, aparecerá un guión “-”.
3. Si la casilla está marcada y (¡atención!) la celda ya contiene un guión “-”, entonces anotamos la fecha y hora de ese instante.
4. Pero si en este punto de la secuencia de decisión resulta que la celda no contiene un guión, eso querrá decir que en algún momento anterior ya se ha escrito en ella la marca de tiempo, por tanto se deja como está. De lo contrario perderíamos la referencia temporal registrada justo tras marcar la casilla.

La parte susceptible de provocar un pequeño colapso mental es 3 - 4, ¡a que sí!

Es ahí donde entra en juego la magia iterativa que permite resolver, para regocijo de propios y extraños, la dependencia circular del modelo de cálculo. Bueno, autocircular, si me permites el palabro, en este caso, dado que el resultado de la fórmula depende del valor que ha devuelto previamente, en la iteración justo anterior.

Con todo lo aprendido hasta el momento estoy seguro de que no te va a costar nada identificar en este caso de uso limitador de velocidad, freno de mano y llave de contacto. Del GPS (contador de iteración) te libras en esta ocasión, no lo necesitamos.

Y cómo no, aquí tienes la plantilla de este control de presencia iterativo, para que le metas mano a tu aire.

Un último detalle.

Verás que en la columna F el tiempo transcurrido no se calcula utilizando una fórmula matricial, con ArrayFormula. No es por vicio ni maldad. Es que solo funciona medio bien y parece ser necesario un paso de cálculo extra para que se aclare y devuelva el resultado que debe. ¿Por qué razón? Vaya usted a saber.

Ya te lo advertí. Los cálculos iterativos tienen su carácter. Pero son buena gente... cuando llegas a conocerlos.

Créditos: La imagen de cabecera utiliza una foto de Max Kobus tomada de Unsplash. Drawing Hands es una litografía de M. C. Escher.