
Midiendo las diferencias entre secuencias de texto usando la distancia de Levenshtein y Apps Script
👇 ¡En resumen! 👇
En este artículo construiremos con Apps Script dos funciones personalizadas para hojas de cálculo de Google que utilizan la distancia de Levenshtein ampliada para determinar la semejanza entre cadenas de texto.
Hacía mucho tiempo que quería escribir sobre el modo de cuantificar las diferencias entre secuencias de texto en nuestras queridas hojas de cálculo de Google. Y esto, ¿para qué sirve?, me parece oírte preguntar al otro lado de la pantalla... Pues para muchas cosas, apreciado ser humano que has decidido acompañarme un rato.
Si somos capaces de reducir a un simple valor numérico las diferencias entre dos cadenas de caracteres dadas, de manera repetible y no ambigua, podremos determinar, por ejemplo, el número de errores que tal vez se hayan deslizado al teclear una determinada palabra o frase.
Más aún, si disponemos de antemano del conjunto completo de secuencias de caracteres válidas en un contexto de uso específico —un diccionario, para que nos entendamos— podemos tratar incluso de adivinar la palabra que el usuario ha querido introducir a pesar de los posibles errores dactilográficos.
Creo que ya debes ver por dónde van los tiros. Los algoritmos que permiten medir lo que se ha venido en denominar, de modo general, distancia de edición entre dos secuencias de texto resultan de gran utilidad en muchas aplicaciones relacionadas con el tratamiento automatizado de la información.

Sin ir más lejos, piensa en correctores ortográficos o sistemas de reconocimiento óptico de caracteres, entre otros casos de uso más esotéricos como pueden ser el cálculo de la inteligibilidad mutua de distintos idiomas o dialectos, la detección de fraudes o incluso la comparación de secuencias de ADN.
Cierto es que la interfaz de usuario de cualquier herramienta digital cuenta con controles de entrada de datos especialmente diseñados para que el usuario pueda seleccionar, en lugar de escribir, uno o varios elementos de entre un conjunto limitado. Estoy hablando, naturalmente, de los familiares cuadros desplegables, elementos de selección múltiple o casillas de verificación, que tan efectivos resultan a la hora de evitar errores de introducción de datos.
Pero también es cierto que a menudo no tendremos más remedio que trabajar en nuestras hojas de cálculo con secuencias de texto que contienen pequeñas erratas. Acompáñame durante los próximos minutos para saber cómo podemos lidiar con ellas.
TABLA DE CONTENIDOS
La distancia de Levenshtein y sus sabores
Una de las métricas más populares para calcular la distancia de edición entre dos cadenas de texto es la distancia de Levenshtein (DL, en adelante). Este artefacto es casi tan viejo como el mundo (1965) y se lo debemos a un matemático ruso de origen judío que se llamaba (sorpresa) Vladimir Levenshtein.
Vladimir dedicó gran parte de su vida a estudiar cosas tan dicharacheras como los códigos de corrección de errores o la teoría de la información. Y teniendo en cuenta que han pasado casi 60 años desde que inventó su famosa distancia, que aún hoy en día sigue usándose, cabe suponer pues que este distinguido caballero realmente estuvo acertado.
En la Wikipedia explican muy bien cómo funciona la DL, pero bueno, por resumir un poco, la idea feliz consiste en transformar una cadena de texto en cualquier otra utilizando una secuencia de longitud mínima formada por una combinación arbitraria de estas tres operaciones de edición atómicas:
🔃 Sustituir un carácter por otro.
➕ Insertar un nuevo carácter.
✂️ Eliminar un carácter ya presente.
El algoritmo de Levenshtein lo que hace, por tanto, es dar con esta secuencia óptima (más corta) de operaciones de edición. Su implementación recursiva en cualquier lenguaje de programación es inmediata, dado que la hermosa (debo decir) definición matemática de la estrategia que caviló este buen hombre allá por los años 60 resulta muy intuitiva.
El problema, como tal vez sepas ya, es que los algoritmos recursivos (como este otro más prosaico) suelen resultar poco eficientes. Por esa razón, gente más inteligente que yo (The String-to-String Correction Problem, Robert A. Wagner y Michael J. Fischer) encontró, hace también un buen montón de años, un modo de transformar esta estrategia recursiva en otra iterativa, no tan intuitiva pero sí más eficiente, basada en técnicas de programación dinámica. De este modo solo hay que montar una matriz, llenarla de numeritos del modo debido y sentarse a recoger la distancia mínima que aparecerá en la celda inferior derecha.
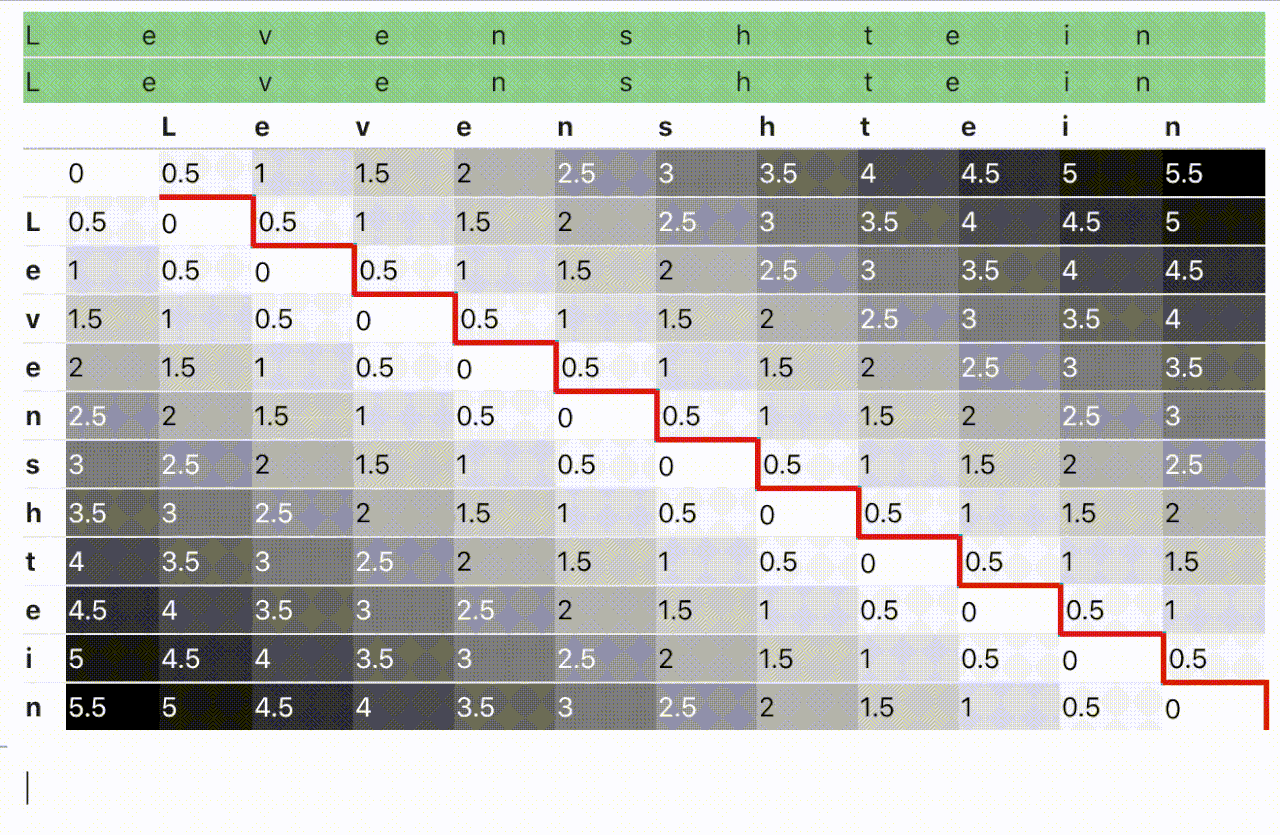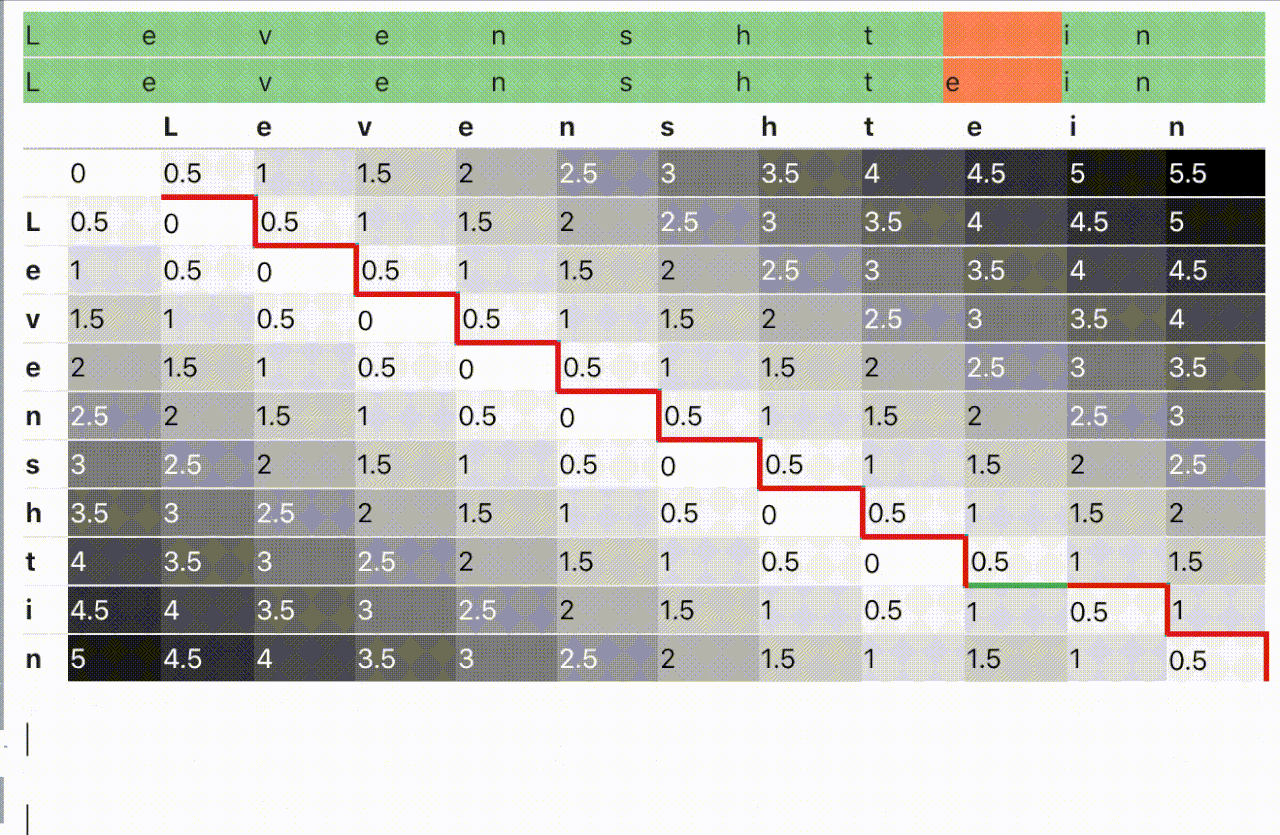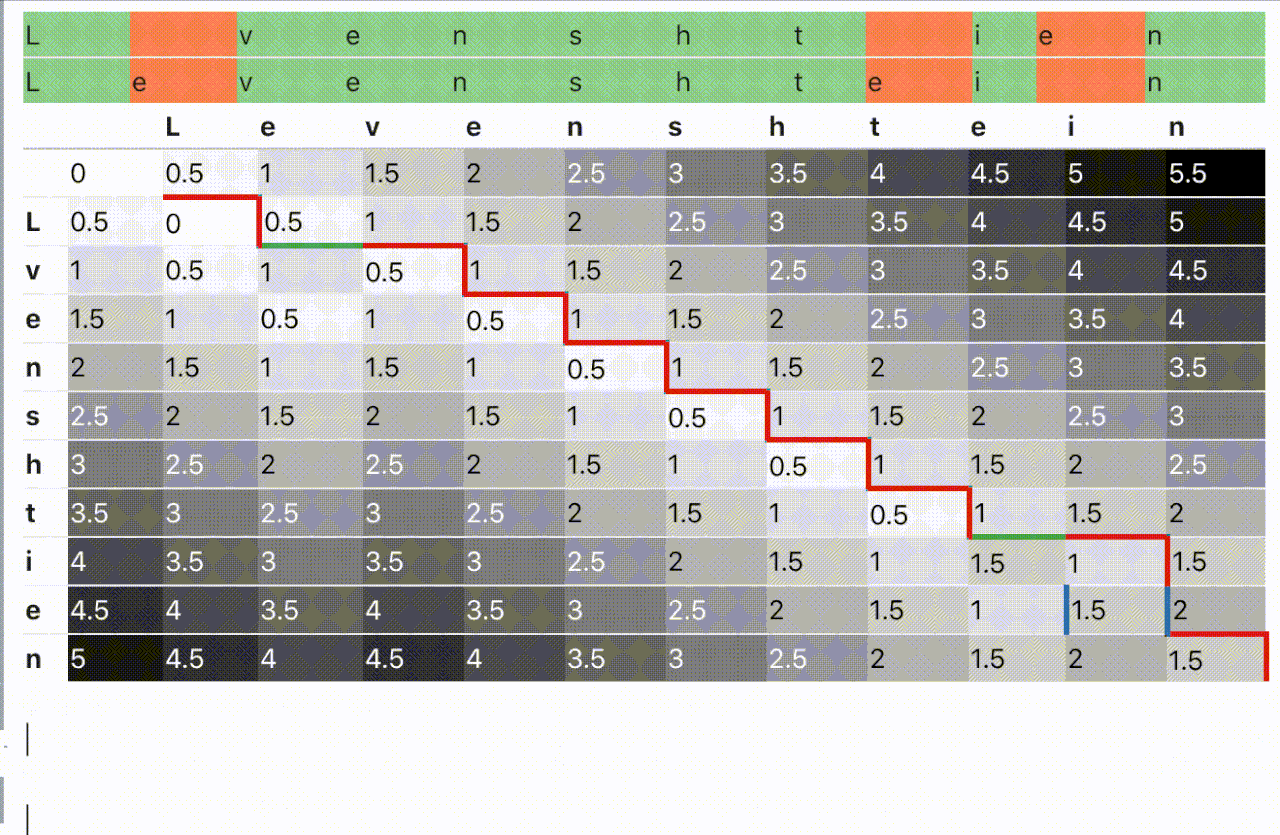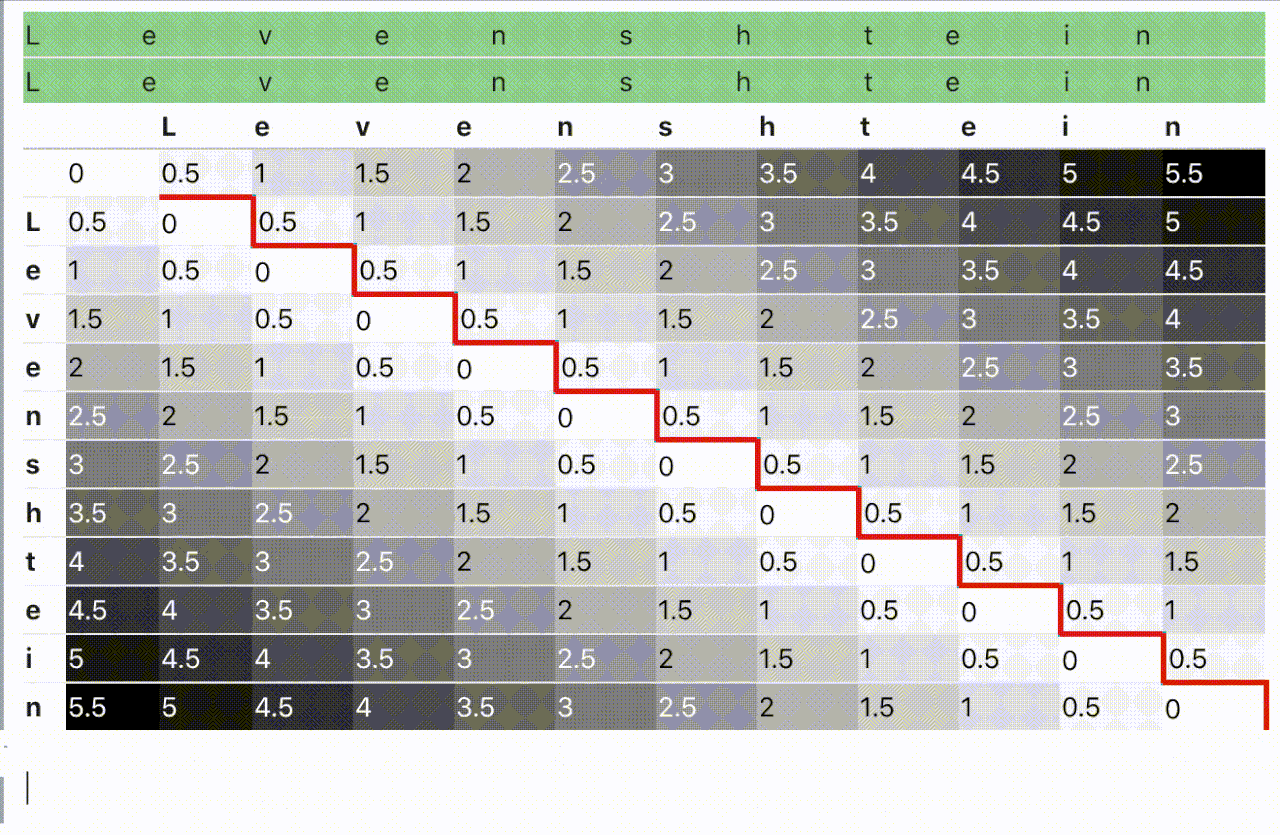
¿Magia? ¡Algoritmia clásica, más bien!
La cosa se puede complicar más, claro (al decir esto no sé por qué me viene siempre a la mente una novela de Jack Williamson titulada Más oscuro de lo que pensáis, ahí lo dejo).
Por ejemplo, probablemente querrás asignar diferentes pesos (costes) a cada una de las operaciones de edición (sustitución, inserción , eliminación). Bueno, pues alguien ya lo hizo por ti, claro está.
¿Y qué me dices de contemplar también la transposición de caracteres como una más de esas operaciones de edición? Pues lo mismo, un tipo llamado Frederick J. Damerau ya pensó en ello y se sacó de la manga algo llamado (¡adivina!) distancia de Damerau - Levenshtein, que se puede abreviar casi recursivamente, cómo mola, como DDL. Y por cierto, esta DDL viene en dos versiones, la "fundamentals" (distancia de alineamiento óptimo de cadenas, también conocida como distancia de edición restringida) y la "plus" (distancia de Damerau - Levenshtein con múltiples transposiciones adyacentes).
Pues sí, un festival.
Y para rematar toda esta cadena de ideas felices, alguien pensó también en que eso de usar una matriz de tantísimas celdas, tantas como el producto de las longitudes de las cadenas a comparar, estaba un poco feo. Y se dio cuenta de que realmente solo eran necesarias dos filas (tres a lo sumo, como será en nuestro caso) para realizar en modo eco el cálculo iterativo hasta el resultado numérico final. Grita conmigo, ¡viva la reducción de la complejidad espacial!
Te cuento todo esto porque soy incapaz de no hacerlo y lanzarme a la implementación sin más. El contexto es importante para mí. Pero no te molesto más con estas cosas y pasamos ya a la acción.
Lo que vamos a hacer es construir usando Apps Script no una sino dos funciones para las hojas de cálculo de Google que nos permitan sacar partido del cálculo las distancias de edición entre cadenas. Y de paso enredaremos un poco con el código, como siempre.
☝ En este espacio ya he hablado con anterioridad de cómo va eso de las funciones personalizadas para hojas de cálculo, tal vez quieras echar un vistazo antes de seguir.
Implementación de distanciaLevenshtein_()
He dicho que íbamos a implementar dos funciones pero seguramente te habrás dado cuenta de que vienen por delante tres secciones tituladas "implementación". ¡Buena vista!
Nuestras dos funciones van a tener un núcleo común, el motor de cálculo de la distancia de edición. No tiene sentido repetir este código dentro de ambas, así que he pensando que lo mejor sería empaquetarlo dentro de una función auxiliar llamada:
distanciaLevenshtein_()
No sé si sabes que las funciones Apps Script que creas dentro de una hoja de cálculo de Google quedan automáticamente expuestas en el editor como si de funciones nativas pertenecientes al lenguaje de fórmulas se tratara.
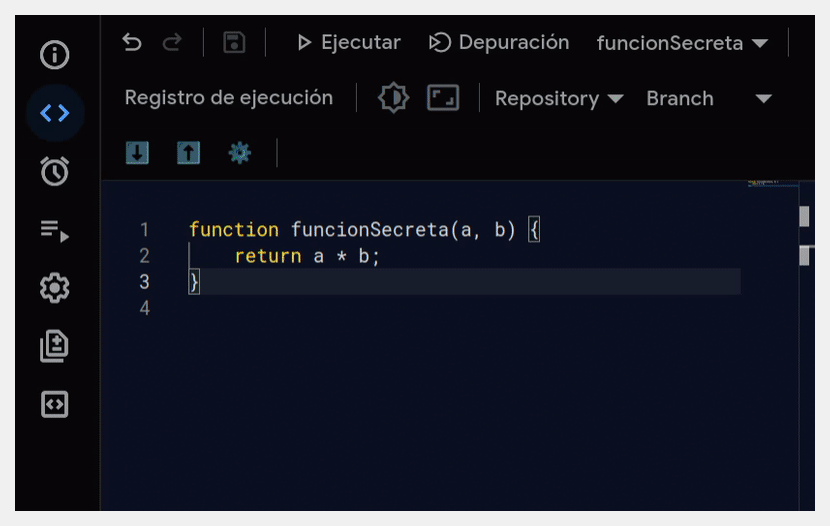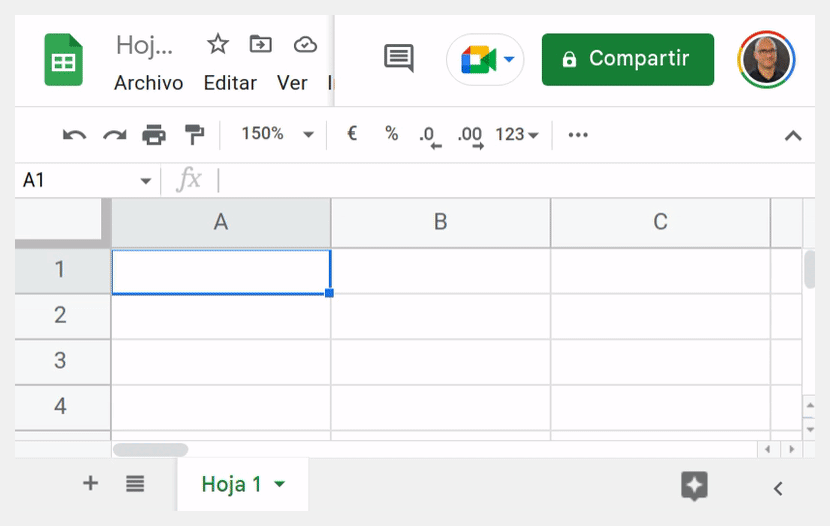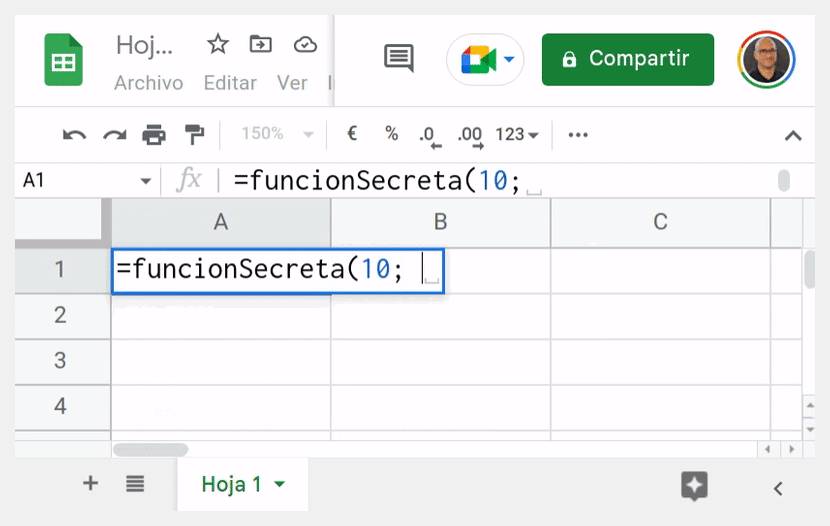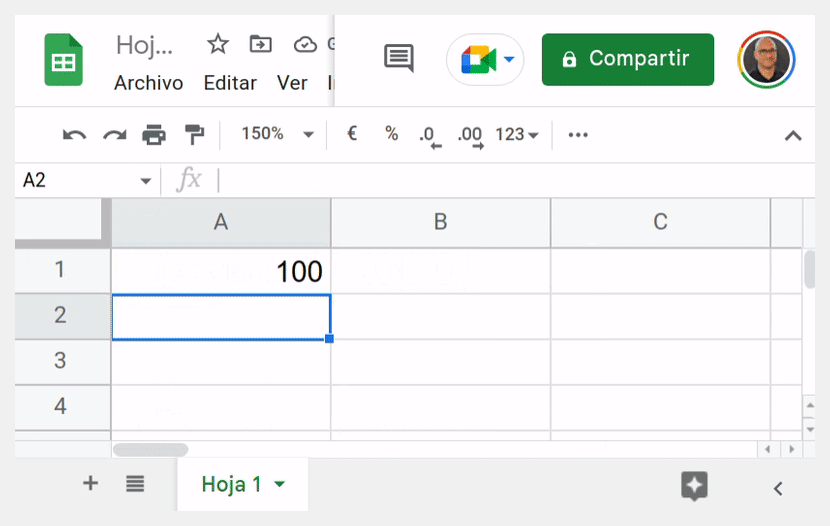
Sí, aunque no añadas una línea de comentario con el consabido @customfunction, que realmente solo sirve para activar el autocompletado y la ayuda contextual de la función, si está disponible.
Por tanto, un hipotético usuario con ganas de enredar solo tiene que averiguar su nombre (basta con husmear en el editor de código) y escribir:
=nombre_funcion_que_no_debes_tocar()
Y esto, como te puedes imaginar, tal vez no sea buena idea.
El código Apps Script de una función personalizada se ejecuta dentro de un entorno mucho más limitado que el que lo hace de manera convencional, por lo que resultan bastante inocuas. Por esta razón, aunque a un usuario curioso le dé por enredar lo más probable es que no ocurra nada catastrófico.
No obstante, lo aconsejable es impedir que las funciones Apps Script que no se hayan usado para implementar funciones personalizadas puedan ser invocadas desde el editor de la hoja de cálculo del modo descrito.
Este se consigue haciendo que estas funciones sean privadas, es decir, usando el carácter "_" como sufijo en su nombre. Así de sencillo.
☝ Esto de las funciones privadas tiene cierta importancia. Por esa razón estoy preparando otro artículo dónde hablaré de ellas con más detenimiento. No te lo pierdas, en él te contaré algunas cosas escalofriantes que les pueden ocurrir a tus scripts si no andas con cuidado (sí, momento de tensión interrumpida vergonzante).
Las dos funciones Apps Script adicionales que implementaremos en los apartados siguientes actuarán realmente como envoltorios para distanciaLevenshtein_(), que la ocultan al mismo tiempo que enriquecen sus funcionalidades con una serie de capacidades adicionales.
En este caso la integridad de nuestros datos no hubiera corrido peligro alguno de haber permitido que un usuario pudiera invocar directamente la función distanciaLevenshtein_(), pero así optimizamos el código y, de paso, introducimos esta buena práctica.
Dentro de esta función vamos a implementar el algoritmo de cálculo de la distancia de edición restringida entre dos secuencias de texto, es decir la versión de la distancia de Damerau - Levenshtein que admite transposiciones, pero solo simples.
Además, vamos a introducir ciertos ajustes que permitan parametrizar su funcionamiento de manera opcional para:
- Usar la distancia de Levenshtein convencional, sin transposiciones.
- Diferenciar o no entre mayúsculas y minúsculas.
- Convertir a texto los valores de entrada cuando no lo sean.
- Asignar pesos a cada una de las operaciones de edición de inserción, eliminación, sustitución y transposición.
Te tiro el código y comentamos cuatro cosas:
/**
* Calcula la distancia de Levenshtein entre dos cadenas de texto. Soporta operaciones de sustitución, eliminación,
* adición y transposiciones no adyacentes de caracteres (versión simple de la distancia de Damerau-Levenshtein
* https://en.wikipedia.org/wiki/Damerau%E2%80%93Levenshtein_distance#Optimal_string_alignment_distance). También puede
* diferenciar o no mayúsculas y minúsculas. Solo utiliza 3 vectores, en lugar de una matriz completa.
* Basada en una ensoñación de ChatGPT (aunque no sin una muy larga y accidentada conversación previa).
*
* Se trata de una función auxiliar privada invocada desde DISTANCIA_EDICION() y DISTANCIA_EDICION_MINIMA()
*
* @param {string} c1 La primera cadena de texto a comparar.
* @param {string} c2 La segunda cadena de texto a comparar.
* @param {boolean} [permiteTrans=true] Admite operaciones de transposición de caracteres. Por defecto, verdadero.
* @param {boolean} [distingueMayusculas=true] Diferencia mayúsculas de minúsculas. Por defecto, verdadero.
* @param {boolean} [fuerzaTexto=true] Indica si se deben tratar de forzar a texto los valores numéricos ([VERDADERO] | FALSO).
* @param {number} [costeIns=1] El valor numérico que representa el coste de la operación de inserción [1].
* @param {number} [costeEli=1] El valor numérico que representa el coste de la operación de eliminación [1].
* @param {number} [costeSus=1] El valor numérico que representa el coste de la operación de sustitución [1].
* @param {number} [costeTrans=1] El valor numérico que representa el coste de la operación de transposición [1].
*
* @return {number} La distancia de Levenshtein entre las dos cadenas de texto.
*/
function distanciaLevenshtein_(
c1, c2,
permiteTrans = true, distingueMayusculas = true, fuerzaTexto = true,
costeIns = 1, costeEli = 1, costeSus = 1, costeTrans = 1
) {
// Se desea forzar conversión a texto de valores numéricos?
if (fuerzaTexto) {
if (typeof c1 == 'number') c1 = String(c1);
if (typeof c2 == 'number') c2 = String(c2);
}
// Si no tenemos cadenas no devolveremos nada de manera explícita
if (typeof c1 == 'string' && typeof c2 == 'string') {
// Tratamiento de mayúsculas
if (!distingueMayusculas) { c1 = c1.toUpperCase(); c2 = c2.toUpperCase(); }
// Inicializar matriz
const matrizDistancias = [[], [], []];
const l1 = c1.length;
const l2 = c2.length;
// Casos base
if (c1 == c2) return 0;
if (l1 == 0) return l2 * costeIns;
if (l2 == 0) return l1 * costeEli;
// Inicializar primera fila de matriz distancias
for (let j = 0; j <= l2; j++) matrizDistancias[0][j] = j * costeIns;
// Cálculo iterativo de las matriz (reducida) de distancias
for (let i = 1; i <= l1; i++) {
// Inicialización de la primera columna
matrizDistancias[i % 3][0] = i * costeEli;
for (let j = 1; j <= l2; j++) {
// Coste mínimo sin transposición
let costeMin = Math.min(
matrizDistancias[(i-1) % 3][j] + costeEli,
matrizDistancias[i % 3][j-1] + costeIns,
matrizDistancias[(i-1) % 3][j-1] + (c1[i-1] == c2[j-1] ? 0 : costeSus),
);
// Tratamiento de transposiciones, si se permiten
if (permiteTrans && i > 1 && j > 1 && c1[i-2] == c2[j-1] && c1[i-1] == c2[j-2]) {
costeMin = Math.min(costeMin, matrizDistancias[(i-2) % 3][j-2] + costeTrans);
}
matrizDistancias[i % 3][j] = costeMin;
}
}
return matrizDistancias[l1 % 3][l2];
}
}
📌 Líneas 1 - 26:
Esta sección contiene los comentarios JSDoc, que siempre conviene incluir por aquello de cuidar a tu yo futuro, que te agradecerá enormemente todas las aclaraciones que ahora le dejes registradas por escrito, así como la propia declaración de la función.
Verás que se utiliza profusamente la sintaxis para especificar valores por defecto en los parámetros que recibe la función, aunque realmente en este caso no resulta algo especialmente útil.
📌 Líneas 28 - 38:
Aquí se realizan una serie de comprobaciones previas sobre las secuencias de texto a comparar y se aplica el tratamiento necesario para diferenciar o no mayúsculas de minúsculas, forzar la conversión a texto de tipos de datos que no lo son.
No se validan sin embargo el resto de parámetros de entrada. No ocuparemos de estas comprobaciones en las funciones - envoltorio que analizaremos en un momento.
📌 Líneas 40 - 52:
Aquí se tratan los casos base (una o más de las cadenas tienen longitud cero) y se inicializa la matriz de valores (matrizDistancias) para que la secuencia de cálculo iterativo que se desarrollará a continuación sobre ella funcione correctamente.
Se usa la versión del algoritmo optimizada para usar una matriz de tamaño reducido, pero en este caso serán necesarias tres filas (en lugar de dos) para acomodar los cálculos relacionados con las operaciones de transposición de caracteres. Estas tres filas van rotando en cada iteración, utilizándose de manera cíclica. Fíjate en el uso del operador módulo [%] a la hora de acceder a los valores de la matriz de distancias.
📌 Líneas 54 - 83 :
Esta sección constituye el nudo gordiano de la función. No, no la vamos a desmenuzar, pero me gustaría que tú sí la examinaras con cierto detenimiento. Estoy seguro de que no te resultará difícil identificar el modo en que se implementa la definición canónica de la DL que veíamos al comienzo de este artículo.
Lo sé, la estrategia basada en sumas de elementos previamente calculados en la matriz de distancias para obtener finalmente esa distancia mínima no es obvia, pero hoy no estamos aquí para hablar de eso. Te remito a los enlaces facilitados más arriba si te apetece profundizar.
Implementación de DISTANCIA_EDICION()
Vamos con la primera de nuestras funciones - envoltorio, que ya quedan expuestas como funciones personalizadas para que el usuario pueda utilizarlas en las fórmulas de sus hojas de cálculo normalmente.
DISTANCIA_EDICION(
c1; c2;
permiteTrans; distingueMayusculas; fuerzaTexto;
costeInsercion; costeEliminacion; costeSustitucion; costeTransposicion
)
Si repasas el apartado anterior, comprobarás que nuestro primer envoltorio cuenta con exactamente los mismos parámetros que la función privada distanciaLevenshtein_(). Probablemente te estarás preguntando entonces en qué se diferencia de ella. Pues en estos dos detalles:
1️⃣ Se añade una capa de ayuda contextual para explicarle al usuario cómo puede utilizar la función de manera efectiva. Debes tener en cuenta que el modo en que se utiliza JSDoc para documentar una función personalizada para hojas de cálculo presenta ciertas particularidades, por lo que si deseas aprovechar al máximo su capacidad deberás saltarte la sintaxis ortodoxa que se utiliza normalmente en las funciones Apps Script convencionales.
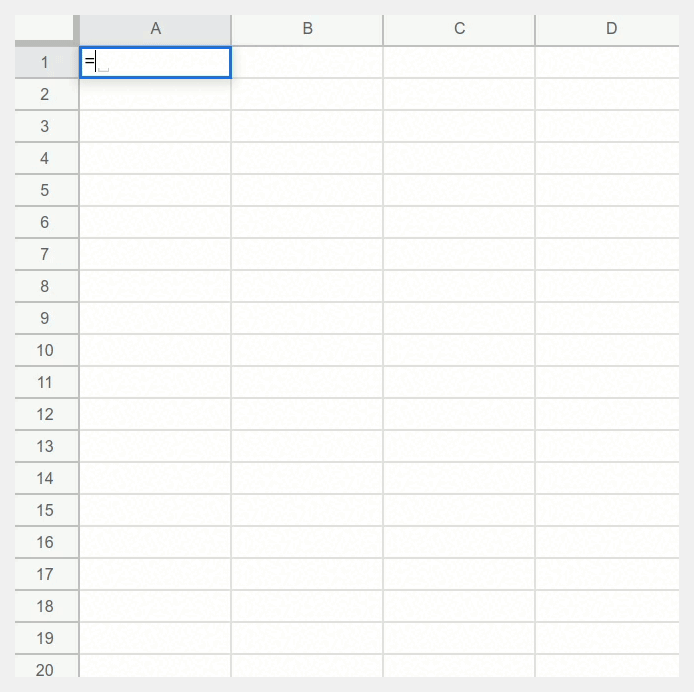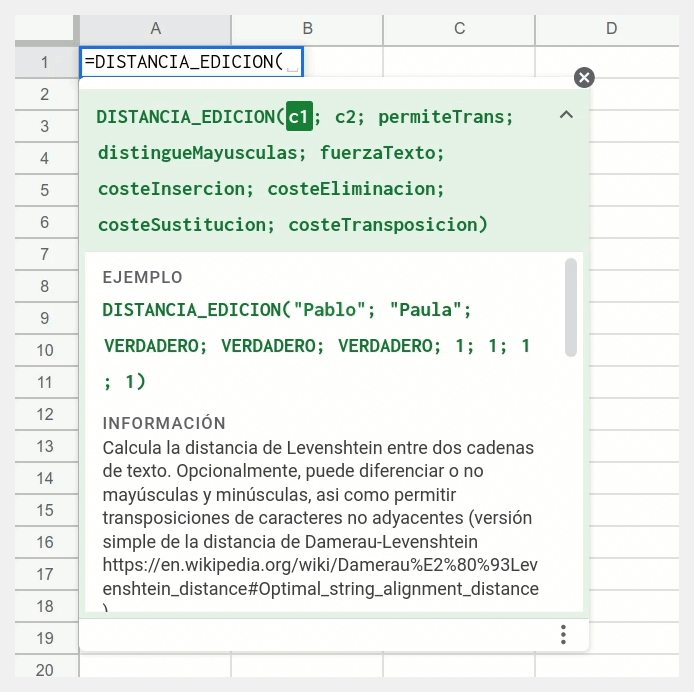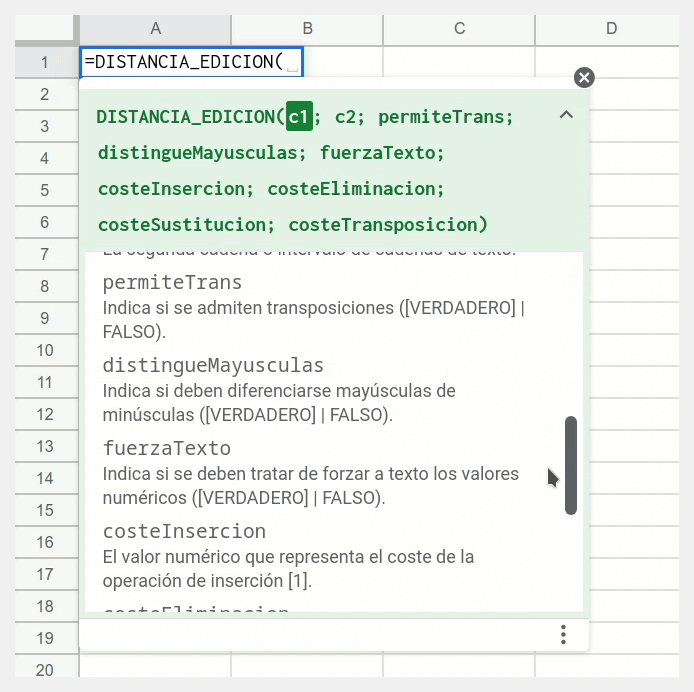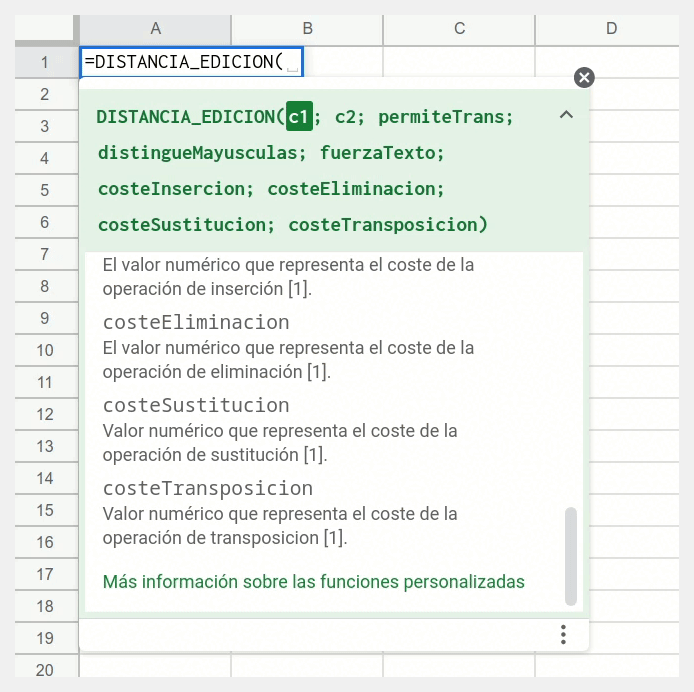
2️⃣ Se incluye el código necesario para que la función sea capaz de calcular la distancia de edición no solo entre dos cadenas de texto sino también entre:
- Una cadena de texto y todas las que se encuentran dentro de un intervalo de datos, tanto si el intervalo se pasa como primer parámetro como en el lugar del segundo. Por ejemplo:
DISTANCIA_EDICION(A2; B2:C10)
DISTANCIA_EDICION(A2:A10; B2)
- Las cadenas de texto de dos intervalos con las mismas dimensiones. En esto caso se comparan, una a una, las cadenas que se encuentran con posición relativa coincidente en ambos intervalos (A2 con B2, A3 con B3,... A10 con B10). Este modo de funcionamiento admite también tanto vectores como matrices.
DISTANCIA_EDICION(A2:A10; B2:B10)
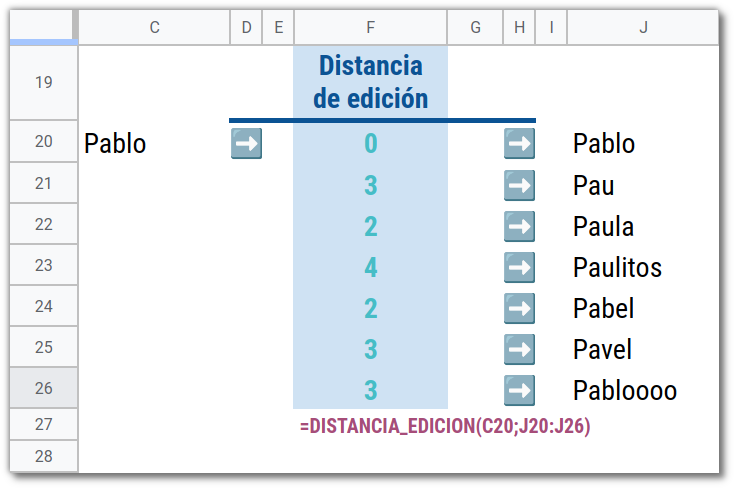
Aunque creo que la ayuda contextual es lo suficientemente explicativa, repasemos brevemente para qué sirven los parámetros admitidos.
| Parámetro | Descripción | Valor si se omite |
| c1, c2 | Cadenas de texto o intervalos de cadenas de texto a comparar. Se admiten tanto rangos como vectores o matrices calculadas. | - |
permiteTrans | Si es VERDADERO se utilizará también la operación de transposición. | VERDADERO |
distingueMayusculas | Si es VERDADERO se diferenciarán mayúsculas de minúsculas. | VERDADERO |
fuerzaTexto | Si es VERDADERO se convertirán los valores que no son de texto a texto para poder ser procesados. | VERDADERO |
costeInsercion, costeEliminacion, costeSustitucion, costeTransposicion | Coste de cada una de las operaciones de edición unitarias. | 1 |
La función permite omitir cualquier parámetro simplemente escribiendo [;]. Los parámetros que no se establezcan de manera explícita asumirán los valores por defecto mostrados en la tabla. Veamos un ejemplo:
DISTANCIA_EDICION("Pablo"; "Pabblo"; ; FALSO)Al invocar la función de este modo:
- Se usarán operaciones de transposición (tercer parámetro omitido, asume un valor por defecto).
- No se deben convertir a texto los valores que no lo son (parámetro fijado de manera explícita a
FALSO), - Se diferenciarán las letras mayúsculas de las minúsculas (cuarto parámetro omitido, asume un valor por defecto).
- El coste de cada operación será de 1 (resto de parámetros omitidos, asumen valores por defecto).
Vamos ahora con la implementación de la función:
/**
* Calcula la distancia de Levenshtein entre dos cadenas de texto. Opcionalmente, puede
* diferenciar o no mayúsculas y minúsculas, asi como permitir transposiciones de caracteres
* no adyacentes (versión simple de la distancia de Damerau-Levenshtein
* https://en.wikipedia.org/wiki/Damerau%E2%80%93Levenshtein_distance#Optimal_string_alignment_distance).
* @param {"Pablo"} c1 La primera cadena o intervalo de cadenas de texto.
* @param {"Paula"} c2 La segunda cadena o intervalo de cadenas de texto.
* @param {VERDADERO} permiteTrans Indica si se admiten transposiciones ([VERDADERO] | FALSO).
* @param {VERDADERO} distingueMayusculas Indica si deben diferenciarse mayúsculas de minúsculas ([VERDADERO] | FALSO).
* @param {VERDADERO} fuerzaTexto Indica si se deben tratar de forzar a texto los valores numéricos ([VERDADERO] | FALSO).
* @param {1} costeInsercion El valor numérico que representa el coste de la operación de inserción [1].
* @param {1} costeEliminacion El valor numérico que representa el coste de la operación de eliminación [1].
* @param {1} costeSustitucion Valor numérico que representa el coste de la operación de sustitución [1].
* @param {1} costeTransposicion Valor numérico que representa el coste de la operación de transposicion [1].
*
* @return La distancia o distancias de edición entre las cadenas comparadas.
*
* @customfunction
*/
function DISTANCIA_EDICION(
c1, c2,
permiteTrans, distingueMayusculas, fuerzaTexto,
costeInsercion, costeEliminacion, costeSustitucion, costeTransposicion
) {
// Comprobación de parámetros y valores por defecto, se hace de este modo para cazar el uso de [;]
// para "saltar" parámetros (se reciben como ''),
permiteTrans = typeof permiteTrans != 'boolean' ? true : permiteTrans;
distingueMayusculas = typeof distingueMayusculas != 'boolean' ? true : distingueMayusculas;
fuerzaTexto = typeof fuerzaTexto != 'boolean' ? true : fuerzaTexto;
costeInsercion = typeof costeInsercion != 'number' ? 1 : costeInsercion;
costeEliminacion = typeof costeEliminacion != 'number' ? 1 : costeEliminacion;
costeSustitucion = typeof costeSustitucion != 'number' ? 1 : costeSustitucion;
costeTransposicion = typeof costeTransposicion != 'number' ? 1 : costeTransposicion;
if (Array.isArray(c1) && Array.isArray(c2)) {
// Intervalo / Intervalo
if (c1.length != c2.length || c1[0].length != c2[0].length) throw 'Las dimensiones de los intervalos que contiene las cadenas de texto no coinciden'
return c1.map((vectorFil, fil) => vectorFil.map((cadena, col) => distanciaLevenshtein_(
cadena, c2[fil][col],
permiteTrans, distingueMayusculas, fuerzaTexto,
costeInsercion, costeEliminacion, costeSustitucion, costeTransposicion
)));
} else if (Array.isArray(c1) && typeof c2 == 'string') {
// Intervalo / Cadena
return c1.map(vectorFil => vectorFil.map(cadena => distanciaLevenshtein_(
cadena, c2,
permiteTrans, distingueMayusculas, fuerzaTexto,
costeInsercion, costeEliminacion, costeSustitucion, costeTransposicion
)));
} else if (typeof c1 == 'string' && Array.isArray(c2)) {
// Cadena / Intervalo
return c2.map(vectorFil => vectorFil.map(cadena => distanciaLevenshtein_(
c1, cadena,
permiteTrans, distingueMayusculas, fuerzaTexto,
costeInsercion, costeEliminacion, costeSustitucion, costeTransposicion
)));
} else if (typeof c1 == 'string' && typeof c2 == 'string' || fuerzaTexto) {
// Cadena / Cadena
return distanciaLevenshtein_(
c1, c2,
permiteTrans, distingueMayusculas, fuerzaTexto,
costeInsercion, costeEliminacion, costeSustitucion, costeTransposicion
);
} else throw 'Error en los parámetros, revisa las cadenas o intervalos de cadenas de texto cuyas distancias deseas medir';
}
📌 Líneas 1 - 25:
Aquí nos encontramos nuevamente con el bloque de líneas de comentarios y la declaración de la función. Nada importante que destacar.
📌 Líneas 27 - 35:
Ahora sí vamos a poner especial cuidado en asegurarnos de que los parámetros introducidos por el usuario sean del tipo correcto. Cuando esto no se cumpla o algunos se hayan omitido se utilizarán una serie de valores por defecto predeterminados.
Me gustaría que repararas en un detalle importante: la función está diseñada para admitir parámetros opcionales, pero en esta ocasión no se usa la sintaxis habitual en la declaración de la función, sino que sus valores predeterminados se establecen más abajo mediante un conjunto de sentencias condicionales como esta:
costeInsercion = typeof costeInsercion != 'number' ? 1 : costeInsercion;
En este caso, si el parámetro costeInsercion contiene un valor de tipo numérico se utilizará sin más. En caso contrario, por ejemplo, cuando se trata de una cadena vacía porque lo hemos omitido al usar la función, se le asignará el valor por defecto (1).
Mi función es muy imaginativa y cuando no le gusta algo se lo inventa. Esta manera de realizar la comprobación de los parámetros opcionales, ciertamente expeditiva, podría refinarse, claro está. En su lugar podríamos haber optado por mostrar mensajes de error diferenciados para cada uno de los parámetros de la función que, sin haber sido omitidos, presentaran valores inapropiados.
Todo esta complicación aparentemente innecesaria se debe a que en ocasiones querremos, al utilizar la función, no asignarle un valor a un parámetro determinado pero sí a otro que viene a continuación. Hemos visto un ejemplo hace un momento, ¿lo recuerdas?
DISTANCIA_EDICION("Pablo"; "Pabblo"; ; FALSO)☝ Cuando usamos [;] para indicar que no estamos interesados en establecer el valor de un parámetro y que pasamos al siguiente, lo que recibe el código de la función no es un valor undefined, que activaría el valor indicado como por defecto en su declaración, sino una cadena vacía.
La estrategia propuesta ofrece una solución flexible para el manejo de argumentos omitidos en las llamadas a las funciones con nombre. Cubre el uso del punto y coma como marcador cuando se omiten de manera selectiva, pero también funciona correctamente cuando se omite el último, sin punto y coma previo, o incluso la totalidad de los argumentos, en cuyo caso la función recibiría valores de tipo indefinido.
Por esa razón, si deseamos que nuestras funciones personalizadas dispongan de esta flexibilidad de uso, no nos quedará más remedio que realizar el control del modo propuesto.
📌 Líneas 37 - 45:
En las cuatro secciones de código que siguen, se tratan los cuatro casos posibles por lo que hace a la naturaleza de los parámetros c1 y c2. En cada una de ellas se llamará a la función privada distanciaLevenshtein_(), que montamos en primer lugar, para calcular las distancias de edición entre las cadenas de texto que corresponda.
Este bloque, en concreto, se ocupa del caso en que ambos parámetros son intervalos de valores (recuerda que deben tener la mismas dimensiones, de lo contrario la función lanzará un mensaje de error).
📌 Líneas 47 - 54 y 56 - 63:
Estos dos bloques, prácticamente idénticos, se ocupan del cálculo cuando uno de los parámetros es una cadena y el otro un intervalo de valores.
📌 Líneas 65 - 76:
Finalmente este bloque se encarga del caso más sencillo, cuando tan solo intervienen dos cadenas de texto. Aquí simplemente se invoca de manera directa la función distanciaLevenshtein_() o se emite un mensaje de error si no nos encontramos en ninguna de las cuatro situaciones admitidas.
¿Todo bien? Pues vamos a por la función que nos falta.
Implementación de DISTANCIA_EDICION_MINIMA()
Eso de poder cuantificar las diferencias entre secuencias de texto está muy bien. Pero se me ocurre que una de las cosas que vas a a querer hacer con este nuevo súper poder en tus hojas de cálculo será usarlo para limpiar tus datos, corrigiendo esos pequeños errores que a menudo se producen al teclear, copiar, pegar, etc.
Tirando de fórmulas convencionales y de la función anterior seguro que podrías lograrlo, con más razón desde que tenemos las maravillosas funciones Lambda y también la posibilidad de definir y guardar funciones con nombre para reutilizarlas en nuestras fórmulas fácilmente, allí donde hagan falta.
Pero aquí hemos venido a explotar Apps Script, así que vamos con una función personalizada más que nos permita satisfacer esta necesidad de un modo directo.
Te presento la función:
DISTANCIA_EDICION_MINIMA(
cadena; referencia;
numCadenas; distanciaMax;
devuelveDistancia; permiteTrans; distingueMayusculas; fuerzaTexto;
costeInsercion; costeEliminacion; costeSustitucion; costeTransposicion
)
Como ves la sintaxis es muy similar a DISTANCIA_EDICION(), pero ahora tenemos tres parámetros adicionales.
☝ Lo que va a hacer esta función es comparar una cadena (o intervalo de cadenas) con una serie de secuencias de texto de referencia usando la ya familiar distancia de edición y devolver una lista ordenada de las cadenas más próximas, es decir, las que se le parecen más.

Podremos además limitar el número de cadenas del conjunto de referencia a devolver de dos maneras diferentes:
- Indicando la cantidad (parámetro numCadenas).
- Indicando la distancia máxima admitida (parámetro distanciaMax).
Los criterios se aplican en el orden indicado: primero se limita por número de resultados (en caso de empate se utiliza un criterio alfabético) y a continuación, si se desea, también teniendo en cuenta la distancia máxima de edición establecida.
La función también es capaz de facilitarnos la distancia de edición de cada una de las cadenas de referencia que se devuelven como resultado en una columna adicional. Para ello hay que establecer el parámetro devuelveDistancia a VERDADERO.

Esta función también cuenta con una generosa ayuda contextual, no obstante no está de más que recojamos en esta los parámetros que admite.
| Parámetro | Descripción | Valor si se omite |
| cadena | Cadena o intervalos de cadenas de texto de las que se quieren obtener cadenas similares. | - |
| referencia | Intervalo de cadenas de texto de referencia a comparar. | - |
| numCadenas | Número de cadenas de referencia similares que se desea obtener. | 1 |
| distanciaMax | Distancia máxima admitida de las cadenas de referencia devueltas. Si se indica un 0 no se establece ningún límite. | 0 |
| devuelveDistancia | Si es VERDADERO la función devolverá una columna adicional en la que se muestran las distancias de edición de las cadenas de referencia devueltas por la función. | FALSO |
permiteTrans | Si es VERDADERO se utilizará también la operación de transposición. | VERDADERO |
distingueMayusculas | Si es VERDADERO se diferenciarán mayúsculas de minúsculas. | VERDADERO |
fuerzaTexto | Si es VERDADERO se convertirán los valores que no son de texto a texto para poder calcular las distancias de edición correspondientes. | VERDADERO |
costeInsercion, costeEliminacion, costeSustitucion, costeTransposicion | Coste de cada una de las operaciones de edición unitarias. | 1 |
Y cómo no, echémosle un vistazo al código, que en esta ocasión en un poco más extenso.
/**
* Devuelve la cadena o cadenas más próximas a una o más específicas, de acuerdo con la distancia de Levenshtein,
* de entre un conjunto de secuencias de texto de referencia candidatas. Opcionalmente, puede diferenciar o no mayúsculas
* y minúsculas, así como permitir transposiciones de caracteres no adyacentes, (versión simple de la distancia de Damerau-Levenshtein
* https://en.wikipedia.org/wiki/Damerau%E2%80%93Levenshtein_distance#Optimal_string_alignment_distance).
*
* @param {"Pablo"} cadena La primera cadena o intervalo de cadenas de texto.
* @param {B2:B10} referencia El intervalo de cadenas de texto de referencia.
* @param {3} numCadenas Nº de cadenas a devolver, en orden creciente de distancia, tiene precedencia sobre distanciaMax [1].
* @param {5} distanciaMax Distancia de edición máxima permitida a las cadenas del conjunto de referencia a devolver, si es 0 sin límite [0].
* @param {FALSO} devuelveDistancia Indica si también se debe devolver la distancia calculada para cada valor de referencia (VERDADERO | [FALSO]).
* @param {VERDADERO} permiteTrans Indica si se admiten transposiciones ([VERDADERO] | FALSO).
* @param {FALSO} distingueMayusculas Indica si deben diferenciarse mayúsculas de minúsculas ([VERDADERO] | FALSO).
* @param {VERDADERO} fuerzaTexto Indica si se deben tratar de forzar a texto los valores numéricos ([VERDADERO] | FALSO).
* @param {1} costeInsercion El valor numérico que representa el coste de la operación de inserción [1].
* @param {1} costeEliminacion El valor numérico que representa el coste de la operación de eliminación [1].
* @param {1} costeSustitucion El valor numérico que representa el coste de la operación de sustitución [1].
* @param {1} costeTransposicion El valor numérico que representa el coste de la operación de transposicion [1].
*
* @return Lista de cadenas similares de la longitud indicada, ordenada por distancia (creciente) + distancia numérica (opcional).
*
* @customfunction
*/
function DISTANCIA_EDICION_MINIMA(
cadena, referencia, numCadenas, distanciaMax,
devuelveDistancia, permiteTrans, distingueMayusculas, fuerzaTexto,
costeInsercion, costeEliminacion, costeSustitucion, costeTransposicion
) {
// Comprobación de parámetros y valores por defecto, se hace de este modo para cazar el uso de [;]
// para "saltar" parámetros (se reciben como ''),
numCadenas = Math.abs(Math.trunc((typeof numCadenas != 'number' || numCadenas < 1 ? 1 : numCadenas)));
distanciaMax = Math.abs(Math.trunc((typeof distanciaMax != 'number' || distanciaMax < 1 ? 0 : distanciaMax)));
devuelveDistancia = typeof devuelveDistancia != 'boolean' ? false : devuelveDistancia;
permiteTrans = typeof permiteTrans != 'boolean' ? true : permiteTrans;
distingueMayusculas = typeof distingueMayusculas != 'boolean' ? true : distingueMayusculas;
fuerzaTexto = typeof fuerzaTexto != 'boolean' ? true : fuerzaTexto;
costeInsercion = typeof costeInsercion != 'number' ? 1 : costeInsercion;
costeEliminacion = typeof costeEliminacion != 'number' ? 1 : costeEliminacion;
costeSustitucion = typeof costeSustitucion != 'number' ? 1 : costeSustitucion;
costeTransposicion = typeof costeTransposicion != 'number' ? 1 : costeTransposicion;
/**
* Función auxiliar, devuelve las distancias medidas entre una cadena de texto dada y cada una
* de las cadenas de texto facilitadas en un array de candidatas, en orden creciente y, en caso
* de empate, de posición en el vector.
*
* @param {string} cadena Cadena a comprobar
* @param {string[][]} referencia Matriz de cadenas candidatas
*
* @return {Object[]} Vector de objetos { cadena_candidata, distancia }
*/
function obtenerDistancias(cadena, referencia) {
// Se admiten que el intervalo que contiene las celdas con las cadenas de referencia sea bidimensional
return referencia.map(vectorFil => vectorFil.map(candidata => (
{
cadena: candidata,
distancia: distanciaLevenshtein_(
cadena, candidata,
permiteTrans, distingueMayusculas, costeInsercion, costeEliminacion, costeSustitucion, costeTransposicion
)
}
))).flat()
// Ordenar por distancia (creciente) + alfabético (ascendente)
.sort((cadena1, cadena2) => cadena1.distancia == cadena2.distancia
? cadena1.cadena.localeCompare(cadena2.cadena)
: cadena1.distancia - cadena2.distancia
)
// Recortar longitud de respuesta
.slice(0, numCadenas)
// Limitar a cadenas dentro de la distancia especificada, si se ha escogido (distanciaMax > 0)
.filter(cadena => distanciaMax == 0 ? true : cadena.distancia <= distanciaMax);
}
if (Array.isArray(cadena) && Array.isArray(referencia)) {
// Cadena / Intervalo
// Se utilizan 2 reduce() anidados para construir la matriz resultado dado que puede tener dimensiones
// distintas a la matriz de cadenas a tratar según parámetro cadena, dependiendo de parámetros numCadenas y devuelveDistancia.
const resultado = cadena.reduce((resultado, vectorFil) => resultado.concat(
vectorFil.reduce((resultadoFil, cadena) => {
const resultadoCadena = obtenerDistancias(cadena, referencia)
.map(candidata => devuelveDistancia ? [candidata.cadena, candidata.distancia] : [candidata.cadena]);
// Expandir matriz resultado parcial añadiendo las columnas necesarias
return resultadoFil.length == 0
? resultadoCadena
: resultadoFil.map((fila, nFil) => fila.concat(resultadoCadena[nFil]));
}, [])
), []);
return resultado;
} else if (typeof cadena == 'string' && Array.isArray(referencia)) {
// Intervalo / Intervalo
return obtenerDistancias(cadena, referencia).map(candidata => devuelveDistancia ? [candidata.cadena, candidata.distancia] : candidata.cadena);
} else throw 'Error en los parámetros, revisa las cadenas o intervalos de cadenas de texto cuyas distancias deseas medir';
}
📌 Líneas 1 - 28:
Comentarios y declaración de la función. Ya sabemos de qué va esto. Siguiente.
📌 Líneas 30 - 41:
Comprobación de los parámetros que ha facilitado el usuario y establecimiento, en su caso, de valores por defecto para los que son opcionales. Tampoco nada nuevo bajo el sol aquí.
📌 Líneas 43 - 75:
Esto sí que es nuevo.
Aquí nos encontramos con la función interna auxiliar obtenerDistancias(), que será utilizada en los dos casos posibles que contempla DISTANCIA_EDICION_MINIMA() por lo que hace a la naturaleza del parámetro cadena, que como ya sabemos puede representar una cadena única o un intervalo de datos con múltiples cadenas de texto.
Esta función recibe una cadena de texto (en ningún caso un intervalo) y construye una lista ordenada con las cadenas de referencia más próximas de acuerdo con su distancia de edición, que calcula utilizando (sorpresa) nuestra función privada distanciaLevenshtein_().
También devolverá, cuando se le requiera, esa columna adicional de la que te he hablado hace un momento que contiene las propias distancias calculadas.
📌 Líneas 77 - 93:
Este es el caso más complicado.
Aquí se compara cada una de las secuencias de texto del intervalo indicado por el parámetro cadena con el conjunto de cadenas de referencia.
La dificultad estriba en que la matriz de datos resultante tendrá a menudo unas dimensiones distintas de la del intervalo de cadenas de entrada a procesar, por lo que serán necesarias algunas filigranas a la hora de construir la estructura matricial de datos que se tiene que devolver. Nada que un par de reduce() anidados no puedan solucionar.
No obstante, te proporciono también una versión alternativa de este bloque que utiliza sendos forEach(). Tal vez resulte un poco más digerible 🤔.
let resultado = [];
cadena.forEach(vectorFil => {
let resultadoFil = [];
vectorFil.forEach(cadena => {
const resultadoCadena = obtenerDistancias(cadena, referencia)
.map(candidata => devuelveDistancia ? [candidata.cadena, candidata.distancia] : [candidata.cadena]);
// Expandir matriz resultado parcial añadiendo las columnas necesarias
resultadoFil = resultadoFil.length == 0
? resultadoCadena
: resultadoFil.map((fila, nFil) => fila.concat(resultadoCadena[nFil]));
});
// Expandir matriz resultado general añadiendo filas
resultado = resultado.concat(resultadoFil);
});
return resultado;
📌 Líneas 95 - 101:
Y hemos dejado lo más fácil para el final.
Aquí se va a procesar una cadena única, por lo que el trabajo se reduce a llamar a la función interna auxiliar obtenerDistancias()... o emitir un mensaje de error si de alguna manera nos encontráramos en una situación no contemplada.
Comentarios finales y siguientes pasos
En esta hoja de cálculo encontrarás el código y algunos ejemplos de uso de las funciones que te he presentado:
No obstante, si te planteas utilizarlas de manera habitual te sugiero que instales mi complemento HdC+, que incluye estas funciones además de muchas otras herramientas que hacen la vida más fácil a la hora de usar las hojas de cálculo de Google.

Debo confesar que he disfrutado mucho preparando este artículo, por mucha razones.
Tras unos meses de enero y febrero muy ajetreados colaborando en la organización de Impulsado DigCompEdu y Comunidad, Reflexión, Acción, en los que he tenido además la suerte de poder impartir sendos talleres sobre Apps Script , me apetecía mucho volver a mi GAS-cueva para retomar proyectos, artículos y otros aprendizajes. En cualquier caso y como siempre, gracias infinitas a mis compañeros del equipo de coordinación de GEG Spain (ahora asociación profesional) por dejarme estar ahí.
Pero es que además, como te contaba al comienzo de este artículo, unir Levenshtein y Apps Script era para mí una asignatura pendiente desde que hace ya muchos meses encontré, en la que fuera mi casa familiar, este trabajo sobre el problema de la corrección cadena - cadena procedente de mi añorada (a menudo por lo que nunca fue) época universitaria en la Facultad de Informática.

Trabajo que, dicho sea de paso, contiene una definición mucho más formal y rigurosa tanto del problema que hemos abordado hoy como de algunas de sus posibles soluciones, ¡implementadas en C! Sí, en los 90 programabas en C o corrías el riesgo de ser considerado un fraude.
Volviendo al asunto que nos ocupa, aún me quedan un par (o tres) de cosas que decir antes de despedirme por hoy.
Por un lado, y poniendo sobre la mesa cuestiones más bien de índole técnica, habrás comprobado que el diseño de funciones personalizadas Apps Script para hojas de cálculo de Google alberga una serie de rincones pintorescos: limitaciones intrínsecas a la hora de acceder a servicios de Google, el sistema de ayuda contextual, las diferentes estrategias de implementación de parámetros opcionales, y su generalización para admitir datos de entrada de tipo matricial (algo en lo que insisten las guías que encontrarás en la documentación oficial de Google, en mi opinión de un modo excesivamente general).
Por otro lado, hemos hablado también de funciones privadas en el contexto de la implementación de funciones personalizadas para hojas de cálculo y de como usarlas para crear envoltorios que abstraigan y aíslen las primeras. Pero la cosa no acaba ni mucho menos con las funciones personalizadas.
Creo que estas dos cuestiones se merecen un artículo (cada una), que ya estoy preparando 👨🍳, así que atento/a a este espacio.
Finalmente, debo decir que esta ha sido la primera vez que he utilizado GPT-3 para generar código. Ya ves, tiene que haber una primera vez para todo.
Pues sí, esto de los modelos de lenguaje natural a gran escala ha surgido ¿de la nada? para revolucionar el mundo. Te podrá gustar más o menos, pero su impacto económico, social, empresarial, en el mundo artístico o educativo... a cinco o diez años vista aún resulta difícilmente cuantificable. Una cosa sí parece segura: será enorme.
El caso es que aunque los algoritmos para calcular la distancia de Levenshtein (y similares) son muy conocidos, me empeñé en pedirles, tanto a la IA de Notion como al ChatGPT de OpenAI (que al fin y al cabo son primas hermanos) que me echaran una mano para desarrollar la función auxiliar privada distanciaLevenshtein_().
¿El resultado? Pues francamente, tiene sus luces y sus sombras.
Ya hemos visto que hay muchas variantes de estos algoritmos: iterativos o recursivos, con o sin transposiciones, con costes unitarios o variables para las operaciones de edición, con optimizaciones que reducen su complejidad espacial. Mi objetivo era alcanzar una versión que:
- Admitiese transposiciones.
- Admitiese pesos variables no unitarios.
- Funcionase de manera iterativa pero almacenando en memoria una matriz de tamaño mínimo.
- Expusiera una función personalizada para hojas de cálculo de Google con los debidos comentarios JSDoc.
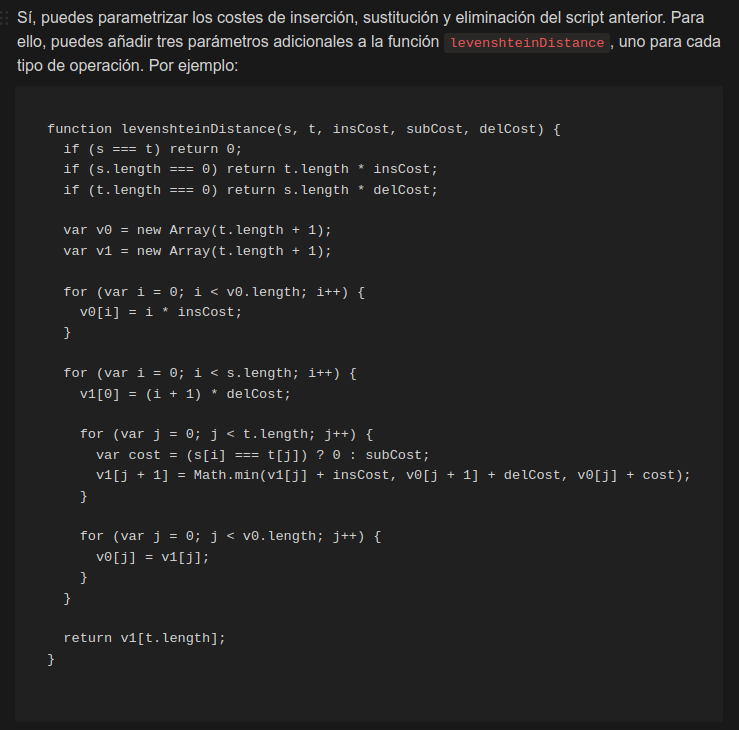
Aunque ambas IAs tenían muy claro por dónde iban los tiros, a menudo se liaban. Al tratar de incluir una mejora incremental sobre cierto código previo olvidaban cosas y dejaban fuera características que sí habían estado presentes en versiones anteriores. Un poco desesperante, la verdad.

En ocasiones también me respondían con código que simplemente no funcionaba correctamente en determinados casos muy específicos. No tuve más remedio que diseñar una batería de pruebas para validar las variadas ensoñaciones que recibía como respuesta a mis probablemente torpes instrucciones.
Sí, las IAs generativas ayudan. Indudablemente. Pero si no sabes lo que haces te puedes ver en un serio problema.
Hablando de dar instrucciones efectivas, tengo la intuición de que muchas de las vías muertas a las que llegué se debieron a mi inexperiencia diseñando prompts eficaces. Me temo que lo del prompt engineering es ya algo contingente.
Haciendo balance, lo cierto es que me hubiera llevado mucho menos tiempo localizar una versión fiable del algoritmo de una fuente contrastada y adaptarlo a mis necesidades.
Tengo que decir que mi opinión sobre estas herramientas maravillosas oscila violentamente en estos momentos entre el escepticismo y la conmoción que supone saberse a ratos viviendo en una de esas novelas de ciencia ficción distópicas con las que me crié. Seguramente la verdad se encuentre en algún punto indeterminado dentro de ese océano de incertidumbre.
Y no, ni NotionAI ni ChatGPT me han proporcionado ideas para preparar este artículo ni mucho menos han escrito una sola línea de él (para bien o para mal 😝).
Una vez más y como siempre, muchas gracias por acompañarme en este pequeño viaje que para mí supone cada nuevo artículo que publico.
Buenas noches y buena suerte, que como especie nos va a hacer mucha falta.
Créditos: La imagen de cabecera utiliza una foto de charlesdeluvio tomada de Unsplash.


Comentarios